Question

【题目】如图，多面体OABCD，AB=CD=2，AD=BC= ，AC=BD= ，且OA，OB，OC两两垂直，则下列说法正确的是（ ）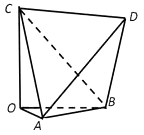
A.直线OB∥平面ACD
B.球面经过点A，B，C，D四点的球的直径是
C.直线AD与OB所成角是45°
D.二面角A﹣OC﹣D等于30°

Answer 1

【答案】B
【解析】解：对于A，由于OB∥AE，AE和平面ACD相交，则OB和平面ACD相交，故A错 对于B，球面经过点A、B、C、D两点的球的直径即为长方体的对角线长，
即为 = ，故B对
对于C由于OB∥AE，则∠DAE即为直线AD与OB所成的角，tan∠DAE= ，则∠DAE=60°，故C错误；
对于D，因为AO⊥OC，DC⊥OC，所以异面直线CD与OA所成的角大小为二面角A﹣OC﹣D的二面角大小，连接OE，则∠AOE为所求，tan∠AOE= ，所以∠AOE=60°；D错误．
故选B．