题目内容
13.已知数列{an}的前三项依次为-2,2,6,且前n项和Sn是n的不含常数顶的二次函数,则a100=394.分析 根据数列的前n项和达式是n的不含常数顶的二次函数,得到数列{an}是等差数列,结合数列{an}的前三项-2,2,6,求出等差数列的通项公式得答案.
解答 解:由题意可设${S}_{n}=a{n}^{2}+bn(a≠0)$,
则a1=S1=a+b,
当n≥2时,an=Sn-Sn-1=(an2+bn)-[a(n-1)2+b(n-1)]=2an-a+b.
验证a1=a+b适合上式.
∴an=2an-a+b.
由an+1-an=2a(n+1)-a+b-2an+a-b=2a为常数.
∴数列{an}是等差数列.
又∵数列{an}的前三项依次为-2,2,6,
∴数列的首项为-2,公差为4,
∴数列{an}的通项公式为:an=4n-6,
∴a100=394.
故答案为:394.
点评 本题考查了数列递推式,考查了等差数列的通项公式与前n项和的表达式,是中档题.

练习册系列答案
相关题目
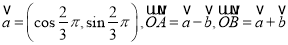 ,若
,若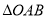 是以
是以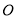 为直角顶点的等腰直角三角形,则
为直角顶点的等腰直角三角形,则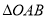 的面积等于( )
的面积等于( ) C.2 D.
C.2 D.