题目内容
18.已知a,b,c分别是△ABC的三个内角A,B,C所对的边,若a=bcos(A+B),则tan(A+$\frac{π}{4}$)的最大值为$\frac{9+4\sqrt{2}}{7}$.分析 a=bcos(A+B)=-bcosC,可得sinA=-sinBcosC,C为钝角,化为tanC=-2tanB.由上面可得:A,B为锐角,tanB>0,tanA>0.可得tanA=-tan(B+C)=$\frac{tanB}{1+2ta{n}^{2}B}$,利用基本不等式的性质即可得出tanA的范围.tan(A+$\frac{π}{4}$)=$\frac{2}{1-tanA}$-1,即可得出最大值.
解答 解:∵a=bcos(A+B)=-bcosC,
∴sinA=-sinBcosC,C为钝角.
∴sin(B+C)+sinBcosC=0,
化为tanC=-2tanB.
由上面可得:A,B为锐角,tanB>0,tanA>0.
∴tanA=-tan(B+C)=-$\frac{tanB+tanC}{1-tanBtanC}$=$\frac{tanB}{1+2ta{n}^{2}B}$=$\frac{1}{\frac{1}{tanB}+2tanB}$≤$\frac{1}{2\sqrt{2}}$,当且仅当tanB=$\frac{\sqrt{2}}{2}$时取等号.
1-tanA≥$1-\frac{1}{2\sqrt{2}}$,
则tan(A+$\frac{π}{4}$)=$\frac{tanA+1}{1-tanA}$=$\frac{2}{1-tanA}$-1≤$\frac{2}{1-\frac{1}{2\sqrt{2}}}$-1=$\frac{9+4\sqrt{2}}{7}$.
∴tan(A+$\frac{π}{4}$)的最大值为$\frac{9+4\sqrt{2}}{7}$.
故答案为:$\frac{9+4\sqrt{2}}{7}$.
点评 本题考查了正弦定理、和差公式、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

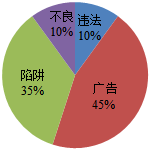 2014年春晚唱响的一曲“群发的我不回”让短信再次成为关注焦点,手机短信中不乏大量垃圾短信,垃圾短信一般分为不良短信、广告短信、违法短信、陷阱短信等四类,其分布如图.
2014年春晚唱响的一曲“群发的我不回”让短信再次成为关注焦点,手机短信中不乏大量垃圾短信,垃圾短信一般分为不良短信、广告短信、违法短信、陷阱短信等四类,其分布如图.| 条数 | [0,5) | [5,10) | [10,15) | [15,20) | [20,25) | [25,30) |
| 人数 | 1 | 2 | 5 | 9 | 5 | 2 |
(1)在这些人中任取一位,接到的垃圾短信低于15条的概率是多少?
(2)估计垃圾短信条数不低于20条的人中每人在一月内接到的广告短信的条数;
(3)为进一步了解这些垃圾短信的分类信息,再从条数在[25,30)中的人甲、乙中选出1位,从条数在[20,25)中的人丙、丁、戊、己、庚中选出2位进行试验研究,求甲和丁同时被选到的概率.
 是纯虚数,则实数a=( )
是纯虚数,则实数a=( ) D.
D.