题目内容
5.已知函数f(x)=|x-a|,a∈R.(I)若a=2,求不等式f(x)+$\frac{3}{2}$-a≥0的解集;
(Ⅱ)若a≥1,且对任意x∈[1,2],不等式xf(x)+$\frac{3}{2}$≥a恒成立,求实数a的取值范围.
分析 (Ⅰ)原不等式即为|x-2|≥$\frac{1}{2}$,由绝对值不等式 的解法即可得到所求解集;
(Ⅱ)令f(x)=x|x-a|,则由题意可得 fmin(x)≥a-$\frac{3}{2}$,分1≤a≤2和a>2两种情况,分别求出实数a的范围,再取并集即得所求.
解答 解:(Ⅰ)不等式f(x)+$\frac{3}{2}$-a≥0,即为
|x-2|≥$\frac{1}{2}$,解得x≥$\frac{5}{2}$或x≤$\frac{3}{2}$,
则解集为(-∞,$\frac{3}{2}$]∪[$\frac{5}{2}$,+∞);
(Ⅱ)∵a≥1,不等式x|x-a|+$\frac{3}{2}$≥a,
对任意的实数x∈[1,2]恒成立,等价于x|x-a|≥a-$\frac{3}{2}$.
令f(x)=x|x-a|,则有 fmin(x)≥a-$\frac{3}{2}$.
当1≤a≤2时,f(x)=x|x-a|=$\left\{\begin{array}{l}{x(x-a),a≤x≤2}\\{x(a-x),2<x≤a}\end{array}\right.$,
∴fmin(x)=f(a)=0,
∴0≥a-$\frac{3}{2}$,解得a≤$\frac{3}{2}$,
故1≤a≤$\frac{3}{2}$.
当a>2时,f(x)=x(a-x),
此时fmin(x)=f(1)或f(2),
故有 $\left\{\begin{array}{l}{f(1)≥a-\frac{3}{2}}\\{f(2)≥a-\frac{3}{2}}\end{array}\right.$,
即$\left\{\begin{array}{l}{a-1≥a-\frac{3}{2}}\\{2a-4≥a-\frac{3}{2}}\end{array}\right.$,解得a≥$\frac{5}{2}$.
综上可得1≤a≤$\frac{3}{2}$或 a≥$\frac{5}{2}$.
点评 本题考查绝对值不等式的解法,考查不等式恒成立问题的解法,注意运用分类讨论的思想方法,考查运算能力,属于中档题.

 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案| A. | 45° | B. | -50° | C. | -40° | D. | 920° |
| A. | 0⊆A | B. | {0}∈A | C. | ∅∈A | D. | {0}⊆A |
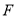 为抛物线
为抛物线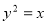 的焦点,点
的焦点,点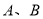 在该抛物线上且位于
在该抛物线上且位于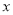 轴的两侧,
轴的两侧,  (其中
(其中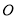 为坐标原点),则
为坐标原点),则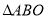 与
与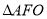 面积之和的最小值是( )
面积之和的最小值是( ) D.
D.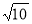
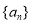 是等差数列,满足
是等差数列,满足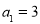 ,
,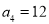 ,数列
,数列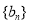 满足
满足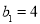 ,
,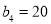 ,且数列
,且数列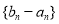 是等比数列.
是等比数列.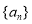 和
和 项和.
项和.