ЬтФПФкШн
9ЃЎвбжЊСНИіЮоЧюЪ§Са{an}ЃЌ{bn}ЗжБ№Тњзу$\left\{\begin{array}{l}{{a}_{1}=1}\\{|{a}_{n+1}-{a}_{n}|=2}\end{array}\right.$ЃЌ$\left\{\begin{array}{l}{{b}_{1}=-1}\\{|\frac{{b}_{n+1}}{{b}_{n}}|=2}\end{array}\right.$ЃЌЦфжаnЁЪN*ЃЌЩшЪ§Са{an}ЃЌ{bn}ЕФЧАnЯюКЭЗжБ№ЮЊSnЁЂTnЃЎЃЈ1ЃЉШєЪ§Са{an}ЃЌ{bn}ЖМЮЊЕндіЪ§СаЃЌЧѓЪ§Са{an}ЃЌ{bn}ЕФЭЈЯюЙЋЪНЃЎ
ЃЈ2ЃЉШєЪ§Са{cn}ТњзуЃКДцдкЮЈвЛЕФе§ећЪ§kЃЈkЁн2ЃЉЃЌЪЙЕУckЃМck-1ЃЌГЦЪ§Са{cn}ЮЊЁАkзЙЕуЪ§СаЁБЃЎ
ЂйШєЪ§Са{an}ЮЊЁА5зЙЕуЪ§СаЁБЃЌЧѓSnЃЎ
ЂкШєЪ§Са{an}ЮЊЁАpзЙЕуЪ§СаЁБЃЌЪ§Са{bn}ЮЊЁАqзЙЕуЪ§СаЁБЃЌЪЧЗёДцдке§ећЪ§mЃЌЪЙЕУSm+1=TmЃЌШєДцдкЃЌЧѓmЕФзюДѓжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЗжЮі ЃЈ1ЃЉгЩСНЪ§СаЮЊЕндіЪ§СаЃЌНсКЯЕнЭЦЪНПЩЕУan+1-an=2ЃЌb2=-2b1ЃЌbn+2=2bn+1ЃЌnЁЪN*ЃЌгЩДЫПЩЕУЪ§Са{an}ЮЊЕШВюЪ§СаЃЌЪ§Са{bn}ДгЕкЖўЯюЦ№ЙЙГЩЕШБШЪ§СаЃЌШЛКѓРћгУЕШВюЪ§СаКЭЕШБШЪ§СаЕФЭЈЯюЙЋЪНЧѓЕУД№АИЃЛ
ЃЈ2ЃЉЂйИљОнЬтФПЬѕМўХаЖЯЃКЪ§Са{an}БиЮЊ1ЃЌ3ЃЌ5ЃЌ7ЃЌ5ЃЌ7ЃЌ9ЃЌ11ЃЌЁЃЌМДЧА4ЯюЮЊЪзЯюЮЊ1ЃЌЙЋВюЮЊ2ЕФЕШВюЪ§СаЃЌДгЕк5ЯюПЊЪМЮЊЪзЯю5ЃЌЙЋВюЮЊ2ЕФЕШВюЪ§СаЃЌЧѓНтSnМДПЩЃЎ
ЂкдЫгУЪ§Са{bn}ЮЊЁАзЙЕуЪ§СаЁБЧвb1=-1ЃЌзлКЯХаЖЯЪ§Са{bn}жагаЧвжЛгаСНИіИКЯюЃЎМйЩшДцдке§ећЪ§mЃЌЪЙЕУSm+1=TmЃЌЯдШЛmЁй1ЃЌЧвTmЮЊЦцЪ§ЃЌЖј{an}жаИїЯюОљЮЊЦцЪ§ЃЌПЩЕУmБиЮЊХМЪ§ЃЎ дйдЫгУВЛЕШЪНжЄУїmЁм6ЃЌЧѓГіЪ§СаМДПЩЃЎ
НтД№ НтЃКЃЈ1ЃЉЁпЪ§Са{an}ЃЌ{bn}ЖМЮЊЕндіЪ§СаЃЌ
ЁргЩЕнЭЦЪНПЩЕУan+1-an=2ЃЌb2=-2b1ЃЌbn+2=2bn+1ЃЌnЁЪN*ЃЌ
дђЪ§Са{an}ЮЊЕШВюЪ§СаЃЌЪ§Са{bn}ДгЕкЖўЯюЦ№ЙЙГЩЕШБШЪ§СаЃЎ
Ёрan=2n-1ЃЌ${b}_{n}=\left\{\begin{array}{l}{-1ЃЌn=1}\\{{2}^{n-1}ЃЌnЁн2}\end{array}\right.$ЃЛ
ЃЈ2ЃЉЂйЁпЪ§Са{an}ТњзуЃКДцдкЮЈвЛЕФе§ећЪ§k=5ЃЌЪЙЕУakЃМak-1ЃЌЧв|an+1-an|=2ЃЌ
ЁрЪ§Са{an}БиЮЊ1ЃЌ3ЃЌ5ЃЌ7ЃЌ5ЃЌ7ЃЌ9ЃЌ11ЃЌЁЃЌМДЧА4ЯюЮЊЪзЯюЮЊ1ЃЌЙЋВюЮЊ2ЕФЕШВюЪ§СаЃЌДгЕк5ЯюПЊЪМЮЊЪзЯю5ЃЌЙЋВюЮЊ2ЕФЕШВюЪ§СаЃЌ
ЙЪ${S}_{n}=\left\{\begin{array}{l}{{n}^{2}ЃЌnЁм4}\\{{n}^{2}-4n+16ЃЌnЁн5}\end{array}\right.$ЃЛ
ЂкЁп$|\frac{{b}_{n+1}}{{b}_{n}}|=2$ЃЌМДbn+1=ЁР2bnЃЌ
Ёр|bn|=2n-1ЃЌ
ЖјЪ§Са{bn}ЮЊЁАзЙЕуЪ§СаЁБЧвb1=-1ЃЌ
ЁрЪ§Са{bn}жагаЧвжЛгаСНИіИКЯюЃЎ
МйЩшДцдке§ећЪ§mЃЌЪЙЕУSm+1=TmЃЌЯдШЛmЁй1ЃЌЧвTmЮЊЦцЪ§ЃЌЖј{an}жаИїЯюОљЮЊЦцЪ§ЃЌ
ЁрmБиЮЊХМЪ§ЃЎ
ЪзЯШжЄУїЃКmЁм6ЃЎ
ШєmЃО7ЃЌЪ§Са{an}жаЃЈSm+1ЃЉmax=1+3+Ё+ЃЈ2m+1ЃЉ=ЃЈm+1ЃЉ2ЃЌ
ЖјЪ§Са{bn}жаЃЌbmБиШЛЮЊе§ЃЌЗёдђ${T}_{m}=-1+{b}_{2}+Ё+ЃЈ-{2}^{m-1}ЃЉ$Ём-1+21+Ё+2m-2+ЃЈ-2m-1ЃЉ=-3ЃМ0ЃЌЯдШЛУЌЖмЃЛ
Ёр$ЃЈ{T}_{m}ЃЉ_{min}=-1+{2}^{1}+Ё+{2}^{m-3}+ЃЈ-{2}^{m-2}ЃЉ+{2}^{m-1}$=2m-1-3ЃЎ
Щш${c}_{m}={2}^{m-1}-ЃЈm+1ЃЉ^{2}-3$ЃЌ
Щш${d}_{m}={c}_{m+1}-{c}_{m}={2}^{m-1}-2m-3$ЃЌ
Жј${d}_{m+1}-{d}_{m}={2}^{m-1}-2ЃО$0ЃЈmЃО7ЃЉЃЌ
Ёр{dm}ЃЈmЃО7ЃЉЮЊдіЪ§СаЃЌЧвd7ЃО0ЃЌдђ{cm}ЃЈmЃО7ЃЉЮЊдіЪ§СаЃЌЖјc8ЃО0ЃЌ
ЁрЃЈTmЃЉminЃОЃЈSmЃЉmaxЃЌ
МДmЁм6ЃЎ
ЕБm=6ЪБЃЌЙЙдьЃК{an}ЮЊ1ЃЌ3ЃЌ1ЃЌ3ЃЌ5ЃЌ7ЃЌ9ЃЌЁЃЌ{bn}ЮЊ-1ЃЌ2ЃЌ4ЃЌ8ЃЌ-16ЃЌ32ЃЌ64ЃЌЁ
ДЫЪБp=2ЃЌq=4ЃЎ
Ёрmmax=6ЃЌЖдгІЕФp=2ЃЌq=4ЃЎ
ЕуЦР БОЬтЪЧаТЖЈвхЬтЃЌПМВщСЫЪ§СаЕнЭЦЪНЃЌзлКЯПМВщбЇЩњдЫгУаТЖЈвхЧѓНтЪ§СаЕФЮЪЬтЃЌПМВщСЫЗжЮіЮЪЬтКЭНтОіЮЪЬтЕФФмСІЃЌЪєгкФбЬтЃЎ

| AЃЎ | tan735ЁуЃОtan800Ёу | BЃЎ | tan1ЃО-tan2 | CЃЎ | tan$\frac{5Іа}{7}$ЃМtan$\frac{4Іа}{7}$ | DЃЎ | tan$\frac{9Іа}{8}$ЃМtan$\frac{Іа}{7}$ |
| AЃЎ | 45Ёу | BЃЎ | -50Ёу | CЃЎ | -40Ёу | DЃЎ | 920Ёу |
| AЃЎ | 0⊆A | BЃЎ | {0}ЁЪA | CЃЎ | ∅ЁЪA | DЃЎ | {0}⊆A |
 ИіАзЧђКЭ
ИіАзЧђКЭ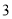 ИіКкЧђЃЌдђЯШУўГіИіАзЧђКѓЗХЛиЃЌдйУўГіИіАзЧђЕФИХТЪЪЧЃЈ ЃЉ
ИіКкЧђЃЌдђЯШУўГіИіАзЧђКѓЗХЛиЃЌдйУўГіИіАзЧђЕФИХТЪЪЧЃЈ ЃЉ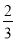 BЃЎ
BЃЎ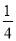 CЃЎ
CЃЎ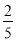 DЃЎ
DЃЎ