题目内容
17.关于下列命题:①存在角α满足$sinα+cosα=\frac{3}{2}$
②函数$y=cos2({\frac{π}{4}-x})$是偶函数;
③函数$f(x)=4sin({2x+\frac{π}{3}})$关于直线$x=-\frac{5π}{12}$对称
④函数$f(x)=4sin({2x+\frac{π}{3}})$可改写为$f(x)=4cos({2x-\frac{π}{6}})$
写出所有正确的命题的题号:③④ (注:把你认为正确的序号都填上)
分析 由条件利用三角函数的图象特征,得出结论.
解答 解:①若存在角α满足$sinα+cosα=\frac{3}{2}$,则1+sin2α=$\frac{9}{4}$,即sin2α=$\frac{5}{4}$ (矛盾),故①不正确.
②由于函数$y=cos2({\frac{π}{4}-x})$=sin2x是奇函数,故②不正确.
③对于函数$f(x)=4sin({2x+\frac{π}{3}})$,令x=-$\frac{5π}{12}$,求得f(x)=-1,为函数的最小值,故函数的图象关于直线$x=-\frac{5π}{12}$对称,故③正确.
④函数$f(x)=4sin({2x+\frac{π}{3}})$=4cos[$\frac{π}{2}$-(2x+$\frac{π}{3}$)]=4cos(2x-$\frac{π}{6}$),故④正确.
故答案为:③④.
点评 本题主要考查三角函数的图象特征,属于基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
7.若圆C与圆(x+2)2+(y-1)2=1关于原点对称,则圆C的方程是( )
| A. | (x-2)2+(y+1)2=1 | B. | (x-2)2+(y-1)2=1 | C. | (x-1)2+(y+2)2=1 | D. | (x+1)2+(y-2)2=1 |
2.已知函数f(x)=Acos(ωx+φ)(A>0,ω>0)的图象与直线y=m(-A<m<0)的三个相邻交点的横坐标分别是3,5,9,则f(x)的单调递增区间是( )
| A. | [6kπ+1,6kπ+4],k∈Z | B. | [6k-2,6k+1],k∈Z | C. | [6k+1,6k+4],k∈Z | D. | [6kπ-2,6kπ+1],k∈Z |
9.已知正方体ABCD-A1B1C1D1,下列向量的数量积不为0的是( )
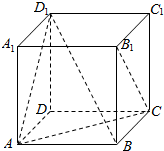

| A. | $\overrightarrow{A{D}_{1}}•\overrightarrow{{B}_{1}C}$ | B. | $\overrightarrow{B{D}_{1}}•\overrightarrow{AC}$ | C. | $\overrightarrow{B{D}_{1}}•\overrightarrow{BC}$ | D. | $\overrightarrow{AB}•\overrightarrow{A{D}_{1}}$ |