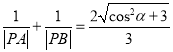题目内容
【题目】在
中，已知
，分别根据下列条件求
（精确到0.01°）.
（1）①
；②
；③
；④
；⑤
；
（2）根据上述计算结果，讨论使有一个解、两个解、无解时，
的取值情况.
【答案】（1）①无解；②
；③
或
；④
；⑤
（2）当
时，无解；当
或
时，有一个解；当
时，有两个解
【解析】
（1）由条件利用正弦定理求得
，再结合大边对大角，判断角
的个数；
（2）结合（1）的结果，讨论使有一解、两解、无解时
的取值情况.
解：（1）根据正弦定理
可得，
，
①当
，
时，
，
因为
且
，所以不存在使得
，即无解；
②当，时，
，
因为且，所以
；
③当
，时，
，
因为且，所以或；
④
，时，
，
因为且，所以或
，
又因为
，所以
，所以，只取；
⑤
，时，
，
因为且，所以或
，
又因为
，所以
，所以，只取.
（2）因为
，
所以，当时，无解；当或时，有一个解；当时，有两个解.
【题目】为了了解某校学生喜欢吃零食是否与性别有关，随机对此校100人进行调查，得到如下的列表：已知在全部100人中随机抽取1人，抽到不喜欢吃零食的学生的概率为
．
喜欢吃零食 | 不喜欢吃零食辣 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 | 100 |
（Ⅰ）请将上面的列表补充完整；
（Ⅱ）是否有99.9%以上的把握认为喜欢吃零食与性别有关？说明理由．
下面的临界值表供参考：
，其中
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
【题目】某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表（假设该区域空气质量指数不会超过300）：
空气质量指数 |
|
|
|
|
|
|
空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
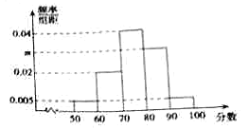
该社团将该校区在2018年11月中10天的空气质量指数监测数据作为样本，绘制的频率分布直方图如下图，把该直方图所得频率估计为概率.
（Ⅰ）以这10天的空气质量指数监测数据作为估计2018年11月的空气质量情况，则2018年11月中有多少天的空气质量达到优良？
（Ⅱ）已知空气质量等级为1级时不需要净化空气，空气质量等级为2级时每天需净化空气的费用为1000元，空气质量等量等级为3级时每天需净化空气的费用为2000元.若从这10天样本中空气质量为1级、2级、3级的天数中任意抽取两天，求这两天的净化空气总费用为3000元的概率.
