题目内容
如图,已知椭圆 过点.
过点. ,离心率为
,离心率为 ,左、右焦点分别为F1、F2.点p为直线l:x+y=2上且不在x轴上的任意一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D,O为坐标原点.
,左、右焦点分别为F1、F2.点p为直线l:x+y=2上且不在x轴上的任意一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D,O为坐标原点.(1)求椭圆的标准方程;
(2)设直线PF1、PF2的斜线分别为k1、k2.①证明:
 ;②问直线l上是否存在点P,使得直线OA、OB、OC、OD的斜率kOA、kOB、kOC、kOD满足kOA+kOB+kOC+kOD=0?若存在,求出所有满足条件的点P的坐标;若不存在,说明理由.
;②问直线l上是否存在点P,使得直线OA、OB、OC、OD的斜率kOA、kOB、kOC、kOD满足kOA+kOB+kOC+kOD=0?若存在,求出所有满足条件的点P的坐标;若不存在,说明理由.
【答案】分析:(1)利用椭圆过已知点和离心率,联立方程求得a和b,则椭圆的方程可得.
(2)①把直线PF1、PF2的方程联立求得交点的坐标的表达式,代入直线x+y=2上,整理求得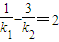 ,原式得证.
,原式得证.
②设出A,B,C,D的坐标,联立直线PF1和椭圆的方程根据韦达定理表示出xA+xB和xAxB,进而可求得直线OA,OB斜率的和与CO,OD斜率的和,由kOA+k)B+kOC+kOD=0推断出k1+k2=0或k1k2=1,分别讨论求得p.
解答:解:(1)∵椭圆过点 ,
,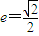 ,
,
∴ ,
,
故所求椭圆方程为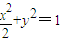 ;
;
(2)①由于F1(-1,0)、F2(1,0),PF1,PF2的斜率分别是k1,k2,且点P不在x轴上,
所以k1≠k2,k1≠0,k2≠0.
又直线PF1、PF2的方程分别为y=k1(x+1),y=k2(x-1),
联立方程解得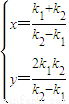 ,
,
所以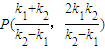 ,由于点P在直线x+y=2上,
,由于点P在直线x+y=2上,
所以 ,
,
故
②设A(xA,yA),B(xB,yB),C(xC,yC),D(xD,yD),联立直线PF1和椭圆的方程得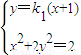 ,
,
化简得(2k12+1)x2+4k12x+2k12-2=0,
因此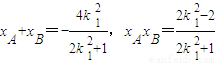 ,
,
所以 ,
,
同理可得: ,
,
故由kOA+k)B+kOC+kOD=0得k1+k2=0或k1k2=1,
当k1+k2=0时,由(1)的结论可得k2=-2,解得P点的坐标为(0,2)
当k1k2=1时,由(1)的结论可得k2=3或k2=-1(舍去),
此时直线CD的方程为y=3(x-1)与x+y=2联立得x=\frac{5}{4}, ,
,
所以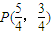 ,
,
综上所述,满足条件的点P的坐标分别为 ,P(0,2).
,P(0,2).
点评:本题主要考查了直线与圆锥曲线的关系的综合问题,椭圆的简单性质.考查了学生综合推理能力,基本计算能力.
(2)①把直线PF1、PF2的方程联立求得交点的坐标的表达式,代入直线x+y=2上,整理求得
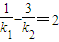 ,原式得证.
,原式得证.②设出A,B,C,D的坐标,联立直线PF1和椭圆的方程根据韦达定理表示出xA+xB和xAxB,进而可求得直线OA,OB斜率的和与CO,OD斜率的和,由kOA+k)B+kOC+kOD=0推断出k1+k2=0或k1k2=1,分别讨论求得p.
解答:解:(1)∵椭圆过点
 ,
,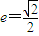 ,
,∴
 ,
,故所求椭圆方程为
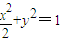 ;
;(2)①由于F1(-1,0)、F2(1,0),PF1,PF2的斜率分别是k1,k2,且点P不在x轴上,
所以k1≠k2,k1≠0,k2≠0.
又直线PF1、PF2的方程分别为y=k1(x+1),y=k2(x-1),
联立方程解得
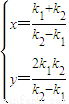 ,
,所以
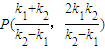 ,由于点P在直线x+y=2上,
,由于点P在直线x+y=2上,所以
 ,
,故

②设A(xA,yA),B(xB,yB),C(xC,yC),D(xD,yD),联立直线PF1和椭圆的方程得
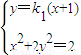 ,
,化简得(2k12+1)x2+4k12x+2k12-2=0,
因此
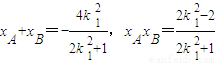 ,
,所以
 ,
,同理可得:
 ,
,故由kOA+k)B+kOC+kOD=0得k1+k2=0或k1k2=1,
当k1+k2=0时,由(1)的结论可得k2=-2,解得P点的坐标为(0,2)
当k1k2=1时,由(1)的结论可得k2=3或k2=-1(舍去),
此时直线CD的方程为y=3(x-1)与x+y=2联立得x=\frac{5}{4},
 ,
,所以
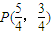 ,
,综上所述,满足条件的点P的坐标分别为
 ,P(0,2).
,P(0,2).点评:本题主要考查了直线与圆锥曲线的关系的综合问题,椭圆的简单性质.考查了学生综合推理能力,基本计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (Ⅱ)试问直线
(Ⅱ)试问直线 过点
过点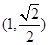 ,离心率为
,离心率为 ,左、右焦点分别为
,左、右焦点分别为 、
、 .点
.点 为直线
为直线 上且不在
上且不在 轴上的任意一点,直线
轴上的任意一点,直线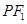 和
和 与椭圆的交点分别为
与椭圆的交点分别为 、
、 和
和 、
、 ,
, 为坐标原点.设直线
为坐标原点.设直线 、
、 .
.
 ;
; 上是否存在点
上是否存在点 、
、 、
、 、
、 的斜率
的斜率 、
、 、
、 、
、 满足
满足 ?若存在,求出所有满足条件的点
?若存在,求出所有满足条件的点 过点.
过点. ,离心率为
,离心率为 ,左、右焦点分别为
,左、右焦点分别为 、
、 .点
.点 为直线
为直线 上且不在
上且不在 轴上的任意一点,直线
轴上的任意一点,直线 和
和 与椭圆的交点分别为
与椭圆的交点分别为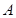 、
、 和
和 、
、 ,
, 为坐标原点.
为坐标原点. 、
、 . 证明:
. 证明:


 过点(1,
过点(1, ),离心率为
),离心率为  .点
.点 为直线
为直线 :
: 上且不在
上且不在 轴上的任意一点,直线
轴上的任意一点,直线 和
和 与椭圆的交点分别为
与椭圆的交点分别为 和
和 为坐标原点.
为坐标原点.

 .
.
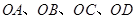 的斜率
的斜率 满足
满足 ?若存在,求出所有满足条件的点
?若存在,求出所有满足条件的点
 过点(1,
过点(1, ),离心率为
),离心率为
 .点
.点 为直线
为直线 :
: 上且不在
上且不在 轴上的任意一点,直线
轴上的任意一点,直线 和
和 与椭圆的交点分别为
与椭圆的交点分别为 和
和 为坐标原点.
为坐标原点. (Ⅰ) 求椭圆的标准方程;
(Ⅰ) 求椭圆的标准方程;
 .
. 证明:
证明:
 的斜率
的斜率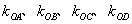 满足
满足 ?若存在,求出所有满足条件的点
?若存在,求出所有满足条件的点