题目内容
如图,已知椭圆
 过点(1,
过点(1, ),离心率为
),离心率为
 ,左右焦点分别为
,左右焦点分别为 .点
.点 为直线
为直线 :
: 上且不在
上且不在 轴上的任意一点,直线
轴上的任意一点,直线 和
和 与椭圆的交点分别为
与椭圆的交点分别为 和
和 为坐标原点.
为坐标原点.
 (Ⅰ) 求椭圆的标准方程;
(Ⅰ) 求椭圆的标准方程;
(Ⅱ)设直线 、
、 斜率分别为
斜率分别为
 .
.
 证明:
证明:
(ⅱ)问直线 上是否存在一点
上是否存在一点 ,
,
使直线 的斜率
的斜率
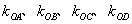 满足
满足 ?若存在,求出所有满足条件的点
?若存在,求出所有满足条件的点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】
【命题意图】本小题主要考查椭圆的基本概念和性质,考查直线与椭圆的位置关系,考查数形结合思想、分类讨论思想以及探求解决新问题的能力。
【解析】(I)解:因为椭圆过点(1,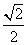 ),e=
),e=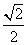 ,
,
所以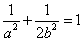 ,
,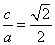 .
.
又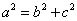 ,
,
所以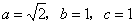
故所求椭圆方程为 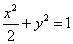 .
.
(II)(i)设点P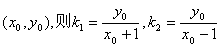 ,因为点P不在x轴上,
,因为点P不在x轴上,
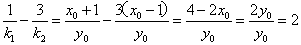 所以
所以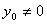 ,又
,又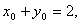
所以
因此结论成立
(ⅱ)解:设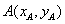 ,
,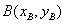 ,
,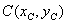 ,
,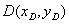 .
.

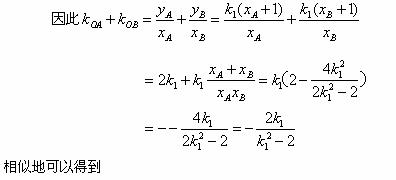

故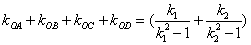
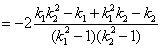

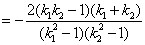
若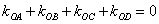 ,须有
,须有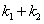 =0或
=0或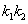 =1.
=1.
① 当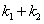 =0时,结合(ⅰ)的结论,可得
=0时,结合(ⅰ)的结论,可得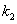 =-2,所以解得点P的坐标为(0,2);
=-2,所以解得点P的坐标为(0,2);
② 当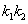 =1时,结合(ⅰ)的结论,可得
=1时,结合(ⅰ)的结论,可得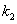 =3或
=3或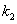 =-1(此时
=-1(此时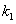 =-1,不满足
=-1,不满足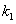 ≠
≠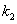 ,舍去 ),此时直线CD的方程为
,舍去 ),此时直线CD的方程为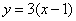 ,联立方程
,联立方程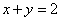 得
得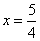 ,
,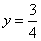
因此 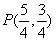 .
.
综上所述,满足条件的点P的坐标分别为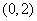 ,(
,(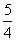 ,
,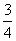 )。
)。

练习册系列答案
相关题目
 (Ⅱ)试问直线
(Ⅱ)试问直线 过点
过点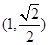 ,离心率为
,离心率为 ,左、右焦点分别为
,左、右焦点分别为 、
、 .点
.点 为直线
为直线 上且不在
上且不在 轴上的任意一点,直线
轴上的任意一点,直线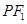 和
和 与椭圆的交点分别为
与椭圆的交点分别为 、
、 和
和 、
、 ,
, 为坐标原点.设直线
为坐标原点.设直线 、
、 .
.
 ;
; 上是否存在点
上是否存在点 、
、 、
、 、
、 的斜率
的斜率 、
、 、
、 、
、 满足
满足 ?若存在,求出所有满足条件的点
?若存在,求出所有满足条件的点 过点.
过点. ,离心率为
,离心率为 ,左、右焦点分别为
,左、右焦点分别为 、
、 .点
.点 为直线
为直线 上且不在
上且不在 轴上的任意一点,直线
轴上的任意一点,直线 和
和 与椭圆的交点分别为
与椭圆的交点分别为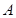 、
、 和
和 、
、 ,
, 为坐标原点.
为坐标原点. 、
、 . 证明:
. 证明:


 过点(1,
过点(1, ),离心率为
),离心率为  .点
.点 为直线
为直线 :
: 上且不在
上且不在 轴上的任意一点,直线
轴上的任意一点,直线 和
和 与椭圆的交点分别为
与椭圆的交点分别为 和
和 为坐标原点.
为坐标原点.

 .
.
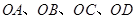 的斜率
的斜率 满足
满足 ?若存在,求出所有满足条件的点
?若存在,求出所有满足条件的点