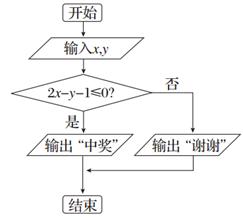
题目内容
(本小题满分13分)
为回馈顾客,某商场拟通过摸球兑奖的方式对1000位顾客进行奖励,规定:每位顾客从一个装有4个标有面值的球的袋中一次性随机摸出2个球,球上所标的面值之和为该顾客所获的奖励额.
(1)若袋中所装的4个球中有1个所标的面值为50元,其余3个均为10元,求
①顾客所获的奖励额为60元的概率
②顾客所获的奖励额的分布列及数学期望;
(2)商场对奖励总额的预算是60000元,并规定袋中的4个球只能由标有面值10元和50元的两种球组成,或标有面值20元和40元的两种球组成.为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡,请对袋中的4个球的面值给出一个合适的设计,并说明理由.
(1)  ,参考解析;(2)参考解析
,参考解析;(2)参考解析
解析试题分析:(1)由袋中所装的4个球中有1个所标的面值为50元,其余3个均为10元,又规定每位顾客从
一个装有4个标有面值的球的袋中一次性随机摸出2个球,球上所标的面值之和为该顾客所获的奖励额..由获得60元的事件数 除以总的事件数
除以总的事件数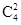 即可. 顾客获得奖励有两种情况20元,60元.分别计算出他们的概率,再利用数学期望的公式即可得结论.
即可. 顾客获得奖励有两种情况20元,60元.分别计算出他们的概率,再利用数学期望的公式即可得结论.
(2) 根据商场的预算,每个顾客的平均奖励为60元.根据题意有两种获奖励的情况,确定符合题意的方案,分别仅有一种.再分别计算出两种方案相应的概率以及求出数学期望和方差.即可得到结论.
试题解析:(1)设顾客所获的奖励为X. ①依题意,得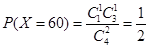 .即顾客所获得的奖励额为60元的概率为
.即顾客所获得的奖励额为60元的概率为 .
.
②依题意,得X的所有可能取值为20,60. 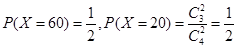 .即X的分布列为
.即X的分布列为
所以顾客所获得的奖励额的期望为X 20 60 P 0.5 0.5 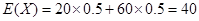 (元).
(元).
(2)根据商场的预算,每个顾客的平均奖励为60元.所以先寻找期望为60元的可能方案.对于面值由10元和50元组成的情况,如果选择(10,10,10,50)的方案,因为60元是面值之和的最大值,所以期望不可能为60元;如果选择(50,50,50,10)的方案,因为60元是面值之和的最小值,所以数学期望也不可能为60元,因此可能的方案是(10,10,50,50),记为方案1.对于面值由20元和40元组成的情况,同理可排除(20,20,20,40)和(40,40,40,20)的方案,所以可能的方案是(20,20,40,40),记为方案2.以下是对两个方案的分析:对于方案1,即方案(10,10,50,50),设顾客所获的奖励为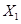 ,则
,则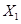 的分布列为
的分布列为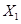
20 60 100 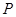
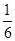
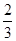
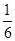
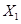 的期望为
的期望为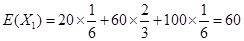 ,
,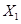 的方差为
的方差为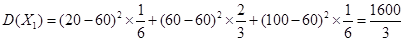 .
.
对于方案2,即方案(20,20,40,40),设顾客所获的奖励为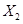 ,则
,则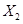 的分布列为
的分布列为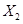
40 60 80 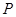
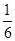
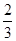
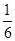
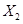 的期望为
的期望为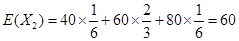 ,
, 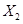 的方差为
的方差为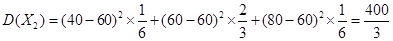 .由于两种方案的奖励额都符合要求,但方案2奖励的方差比方案1的小,所以应该选择方案2.
.由于两种方案的奖励额都符合要求,但方案2奖励的方差比方案1的小,所以应该选择方案2.
考点:1.概率.2.统计.3.数学期望,方差.

某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
| API |  | 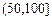 | 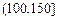 | 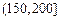 | 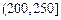 | 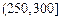 | 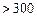 |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
记某企业每天由空气污染造成的经济损失S(单位:元),空气质量指数API为ω。在区间[0,100]对企业没有造成经济损失;在区间
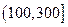 对企业造成经济损失成直线模型(当API为150时造成的 经济损失为500元,当API为200时,造成的经济损失为700元);当API大于300时造成的 经济损失为2000元;
对企业造成经济损失成直线模型(当API为150时造成的 经济损失为500元,当API为200时,造成的经济损失为700元);当API大于300时造成的 经济损失为2000元;(1)试写出是S(ω)的表达式;
(2)试估计在本年内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面2×2列联表,并判断能否有95%的把握认为该市本年空气重度污染与供暖有关?
|
| | 非重度污染 | 重度污染 | 合计 |
| 供暖季 | | | |
| 非供暖季 | | | |
| 合计 | | | 100 |
某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生.
(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据.
甲的频数统计表(部分)
| 运行次数n | 输出y的值 为1的频数 | 输出y的值 为2的频数 | 输出y的值 为3的频数 |
| 30 | 14 | 6 | 10 |
| … | … | … | … |
| 2 100 | 1 027 | 376 | 697 |
乙的频数统计表(部分)
| 运行次数n | 输出y的值 为1的频数 | 输出y的值 为2的频数 | 输出y的值 为3的频数 |
| 30 | 12 | 11 | 7 |
| … | … | … | … |
| 2 100 | 1 051 | 696 | 353 |
当n=2 100时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编程序符合算法要求的可能性较大;
(3)将按程序框图正确编写的程序运行3次,求输出y的值为2的次数ξ的分布列及数学期望.
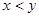 ”
”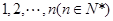 从小到大排列构成一个数
从小到大排列构成一个数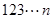 ,
,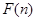 为这个数的位数(如
为这个数的位数(如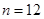 时,此数为
时,此数为 ,共有15个数字,
,共有15个数字, ),现从这个数中随机取一个数字,
),现从这个数中随机取一个数字,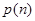 为恰好取到0的概率.
为恰好取到0的概率.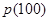 ;
;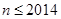 时,求
时,求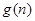 为这个数中数字0的个数,
为这个数中数字0的个数,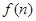 为这个数中数字9的个数,
为这个数中数字9的个数,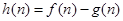 ,
, ,求当
,求当 时
时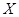 为选出的3名同学中女同学的人数,求随机变量
为选出的3名同学中女同学的人数,求随机变量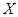 为1名顾客摸奖获得的奖金数额,求随机变量
为1名顾客摸奖获得的奖金数额,求随机变量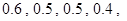 各人是否需使用设备相互独立.
各人是否需使用设备相互独立.