题目内容
某超市在节日期间进行有奖促销,规定凡在该超市购物满400元的顾客,均可获得一次摸奖机会.摸奖规则如下:
奖盒中放有除颜色不同外其余完全相同的4个球(红、黄、黑、白).顾客不放回的每次摸出1个球,若摸到黑球则摸奖停止,否则就继续摸球.按规定摸到红球奖励20元,摸到白球或黄球奖励10元,摸到黑球不奖励.
(1)求1名顾客摸球2次摸奖停止的概率;
(2)记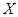 为1名顾客摸奖获得的奖金数额,求随机变量
为1名顾客摸奖获得的奖金数额,求随机变量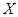 的分布列和数学期望.
的分布列和数学期望.
(1) ; (2)随机变量
; (2)随机变量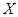 的分布列为:
的分布列为: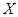

10 20 30 40 





 .
.
解析试题分析:(1)1名顾客摸奖两次盒盖上摸奖的情况有 种,而基本事件和总数有
种,而基本事件和总数有 种,代入等可能事件概率公式可求得;(2)随机变量
种,代入等可能事件概率公式可求得;(2)随机变量 的所有可能取值为0,10,20,30,40,分别求出
的所有可能取值为0,10,20,30,40,分别求出 各取值时的概率即可得.
各取值时的概率即可得.
(1)设“1名顾客摸球2次停止摸奖”为事件A,则 ,
,
故1名顾客摸球2次停止摸奖的概率 . 4分
. 4分
(2)随机变量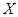 的所有取值为
的所有取值为 .
. ,
, ,
, ,
, ,
, , 8分
, 8分
所以,随机变量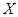 的分布列为:
的分布列为: 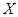

10 20 30 40 





 . 10分
. 10分
考点:(1)古典概型;(2)随机变量的分布列和数学期望.

练习册系列答案
相关题目
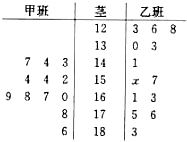
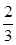 ,乙获胜的概率为
,乙获胜的概率为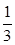 ,各局比赛结果相互独立.
,各局比赛结果相互独立.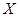 为比赛决出胜负时的总局数,求
为比赛决出胜负时的总局数,求
 ,否则其获胜的概率为
,否则其获胜的概率为 .
.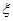 为比赛结束时甲的得分,求随机变量
为比赛结束时甲的得分,求随机变量 .
.