题目内容
(本小题满分14分)
将连续正整数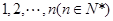 从小到大排列构成一个数
从小到大排列构成一个数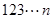 ,
,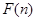 为这个数的位数(如
为这个数的位数(如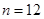 时,此数为
时,此数为 ,共有15个数字,
,共有15个数字, ),现从这个数中随机取一个数字,
),现从这个数中随机取一个数字,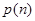 为恰好取到0的概率.
为恰好取到0的概率.
(1)求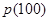 ;
;
(2)当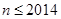 时,求
时,求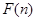 的表达式;
的表达式;
(3)令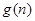 为这个数中数字0的个数,
为这个数中数字0的个数,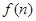 为这个数中数字9的个数,
为这个数中数字9的个数,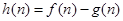 ,
, ,求当
,求当 时
时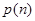 的最大值.
的最大值.
(1) (2)
(2) (3)
(3)
解析试题分析:(1)解概率应用题,关键要正确理解事件. 当 时,这个数中有9个一位数,90个二位数,一个三位数,总共有192个数字,其中数字0的个数为9+2=11,所以恰好取到0的概率为
时,这个数中有9个一位数,90个二位数,一个三位数,总共有192个数字,其中数字0的个数为9+2=11,所以恰好取到0的概率为 (2)按(1)的思路,可分类写出
(2)按(1)的思路,可分类写出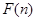 的表达式:
的表达式: ,(3)同(1)的思路,分一位数,二位数,三位数进行讨论即可,当
,(3)同(1)的思路,分一位数,二位数,三位数进行讨论即可,当 当
当 当
当 即
即 同理有
同理有
由 可知
可知 ,当
,当 时,
时, 当
当 时,
时, ,当
,当 时,
时, 由
由 关于k单调递增,故当
关于k单调递增,故当 ,
, 最大值为
最大值为 又
又 ,所以当
,所以当 时,
时, 最大值为
最大值为
试题解析:(1)解:当 时,这个数中总共有192个数字,其中数字0的个数为11,所以恰好取到0的概率为
时,这个数中总共有192个数字,其中数字0的个数为11,所以恰好取到0的概率为 (2)
(2) (3)当
(3)当 当
当 当
当 即
即 同理有
同理有
由 可知
可知 所以当
所以当 时,
时, ,当
,当 时,
时, 当
当 时,
时, ,当
,当 时,
时, 由
由 关于k单调递增,故当
关于k单调递增,故当 ,
, 最大值为
最大值为 又
又 ,所以当
,所以当 时,
时, 最大值为
最大值为
考点:古典概型概率

练习册系列答案
相关题目
 .
.
 、
、 ,他们考核所得的等级相互独立.
,他们考核所得的等级相互独立.