题目内容
1．用反证法证明“若x+y≤0则x≤0或y≤0”时，应假设（ ）| A． | x＞0或y＞0 | B． | x＞0且y＞0 | C． | xy＞0 | D． | x+y＜0 |
分析 熟记反证法的步骤，直接填空即可．反面有多种情况，需一一否定．
解答 解：用反证法证明“若x+y≤0则x≤0或y≤0”时，应先假设x＞0且y＞0．
故选：B．
点评 此题主要考查了反证法的第一步，解此题关键要懂得反证法的意义及步骤．反证法的步骤是：
（1）假设结论不成立；
（2）从假设出发推出矛盾；
（3）假设不成立，则结论成立．
在假设结论不成立时要注意考虑结论的反面所有可能的情况，如果只有一种，那么否定一种就可以了，如果有多种情况，则必须一一否定．
练习册系列答案
相关题目
11．
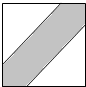如图，在边长为25cm的正方形中挖去边长为23cm的两个等腰直角三角形，现有均匀的粒子散落在正方形中，问粒子落在中间阴影区域的概率是（ ）
如图，在边长为25cm的正方形中挖去边长为23cm的两个等腰直角三角形，现有均匀的粒子散落在正方形中，问粒子落在中间阴影区域的概率是（ ）| A． | $\frac{529}{625}$ | B． | $\frac{96}{625}$ | C． | $\frac{23}{25}$ | D． | $\frac{2}{25}$ |
12．若函数f（x）=ax2-（3a-1）x+a2在[1，+∞）上是增函数，则a的取值范围是（ ）
| A． | 0＜a＜1 | B． | 0≤a≤1 | C． | 0＜a≤1 | D． | 0≤a＜1 |
10．已知函数f （x）是定义在实数集R上不恒为零的偶函数，且f （-1）=0，若对任意的实数x都有xf （x+1）=（1+x） f （x）成立，则$\sum_{k-0}^{2010}f（\frac{k}{2}）$ 的值是（ ）
| A． | 0 | B． | $\frac{1}{2}$ | C． | 1 | D． | $\frac{5}{2}$ |
11．定义在R上的偶函数f（x）满足：对任意的x1，x2∈[0，+∞）（x1≠x2），有$\frac{f（{x}_{2}）-f（{x}_{1}）}{{x}_{2}-{x}_{1}}$＜0．则（ ）
| A． | $f（{0.7^6}）＜f（{log_{0.7}}6）＜f（{6^{0.5}}）$ | B． | f（0.76）＜f（60.5）＜f（log0.76） | ||
| C． | $f（{log_{0.7}}6）＜f（{0.7^6}）＜f（{6^{0.5}}）$ | D． | $f（{log_{0.7}}6）＜f（{6^{0.5}}）＜f（{0.7^6}）$ |