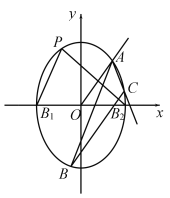题目内容
【题目】已知椭圆![]() ,四点
,四点![]() ,
,![]() ,
,![]() ,
,![]() 中恰有三个点在椭圆
中恰有三个点在椭圆![]() 上,左、右焦点分别为
上,左、右焦点分别为![]() 、
、![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过左焦点![]() 且不与坐标轴平行的直线
且不与坐标轴平行的直线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点,若线段
两点,若线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用椭圆的对称性确定在椭圆上的三点,由椭圆的上顶点![]() 可求出a,点
可求出a,点![]() 或
或![]() 的坐标代入椭圆求出b,即可写出椭圆的方程;(2)联立直线
的坐标代入椭圆求出b,即可写出椭圆的方程;(2)联立直线![]() 的方程与椭圆方程得关于x的一元二次方程,利用韦达定理求出两根之和与两根之积,即可利用弦长公式求出
的方程与椭圆方程得关于x的一元二次方程,利用韦达定理求出两根之和与两根之积,即可利用弦长公式求出![]() ,求出点N的坐标即可写出直线
,求出点N的坐标即可写出直线![]() 的垂直平分线的方程,令
的垂直平分线的方程,令![]() 求出
求出![]() ,代入
,代入![]() 得到关于k的分式,利用基本不等式可求得最小值.
得到关于k的分式,利用基本不等式可求得最小值.
(1)易知![]() ,
,![]() 关于
关于![]() 轴对称,一定都在椭圆上,所以
轴对称,一定都在椭圆上,所以![]() 一定不在椭圆上,根据题意
一定不在椭圆上,根据题意![]() 也在椭圆上,则
也在椭圆上,则![]() ,
,
将![]() 代入椭圆方程得
代入椭圆方程得![]() ,
,
所以椭圆方程为![]() .
.
(2)由![]() 知椭圆的左焦点
知椭圆的左焦点![]() ,
,
设直线![]() 的方程为
的方程为![]() (
(![]() ),
),![]() ,
,![]() ,
,![]() 的中点为
的中点为![]() .
.
联立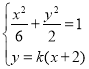 ,可得
,可得![]() ,
,
则![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
点![]()
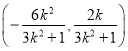 ,
,
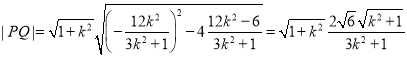
![]() ,
,
![]() 垂直平分线方程为:
垂直平分线方程为:![]() ,
,
令![]() ,求得
,求得![]() ,则
,则![]() ,
,
所以![]()
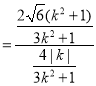
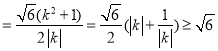 ,当且仅当
,当且仅当![]() 即
即![]() 时取等号,
时取等号,
因此,当![]() ,
,![]() 取最小值
取最小值![]() .
.

练习册系列答案
相关题目
【题目】2016年春节期间全国流行在微信群里发抢红包,现假设某人将688元发成手气红包50个,产生的手气红包频数分布表如下:
金额分组 |
|
|
|
|
|
|
频 数 | 3 | 9 | 17 | 11 | 8 | 2 |
(1)求产生的手气红包的金额不小于9元的频率;
(2)估计手气红包金额的平均数(同一组中的数据用该组区间的中点值作代表);
(3)在这50个红包组成的样本中,将频率视为概率.
①若红包金额在区间![]() 内为最佳运气手,求抢得红包的某人恰好是最佳运气手的概率;
内为最佳运气手,求抢得红包的某人恰好是最佳运气手的概率;
②随机抽取手气红包金额在![]() 内的两名幸运者,设其手气金额分别为
内的两名幸运者,设其手气金额分别为![]() ,
,![]() ,求事件“
,求事件“![]() ”的概率.
”的概率.