题目内容
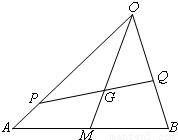
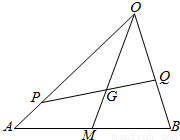 如图,G是△OAB的重心,P、Q分别是边OA、OB上的动点,且P、G、Q三点共线.
如图,G是△OAB的重心,P、Q分别是边OA、OB上的动点,且P、G、Q三点共线.(1)设
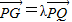 ,将
,将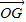 用λ、
用λ、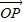 、
、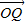 表示;
表示;(2)设
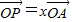 ,
,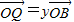 ,证明:
,证明: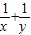 是定值;
是定值;(3)记△OAB与△OPQ的面积分别为S、T.求
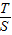 的取值范围.
的取值范围.
【答案】分析:(1)寻找包含 的图形△OPG,利用向量的加法法则知
的图形△OPG,利用向量的加法法则知 ,在根据
,在根据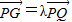 和
和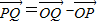 即可
即可
(2)根据(1)结合 ,
, 知:
知: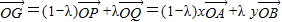 在根据G是△OAB的重心知:
在根据G是△OAB的重心知: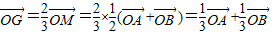 ,最后根据
,最后根据 、
、 不共线得到关于x,y,λ的方程组即可求解
不共线得到关于x,y,λ的方程组即可求解
(3)根据三角形面积计算公式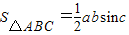 ,知
,知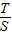 =xy,由点P、Q的定义知
=xy,由点P、Q的定义知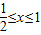 ,
,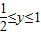 ,
,
且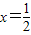 时,y=1;x=1时,
时,y=1;x=1时, .此时,均有
.此时,均有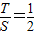 .
.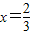 时,
时,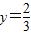 .此时,均有
.此时,均有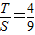 .得到
.得到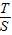 的范围为
的范围为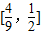 在根据(2)知
在根据(2)知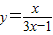 进行作差证明即可
进行作差证明即可
解答:解:(1) =
=
(2)一方面,由(1),得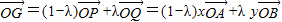 ;①
;①
另一方面,∵G是△OAB的重心,
∴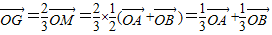 .②
.②
而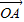 、
、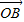 不共线,∴由①、②,
不共线,∴由①、②,
得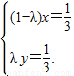
解之,得 ,
,
∴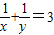 (定值).
(定值).
(3)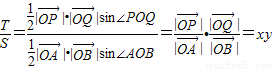 .
.
由点P、Q的定义知 ,
,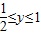 ,
,
且 时,y=1;x=1时,
时,y=1;x=1时,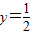 .
.
此时,均有 .
.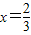 时,
时,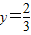 .
.
此时,均有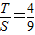 .
.
以下证明: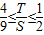 .
.
由(2)知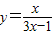 ,
,
∵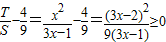 ,
,
∴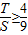 .
.
∵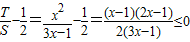 ,
,
∴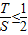 .
.
∴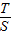 的取值范围
的取值范围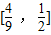 .
.
点评:本题考查了向量的加减法,三角形的面积公式,作差法证明不等式,属于基础题.
 的图形△OPG,利用向量的加法法则知
的图形△OPG,利用向量的加法法则知 ,在根据
,在根据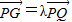 和
和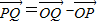 即可
即可(2)根据(1)结合
 ,
, 知:
知: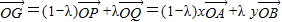 在根据G是△OAB的重心知:
在根据G是△OAB的重心知: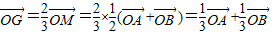 ,最后根据
,最后根据 、
、 不共线得到关于x,y,λ的方程组即可求解
不共线得到关于x,y,λ的方程组即可求解(3)根据三角形面积计算公式
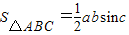 ,知
,知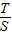 =xy,由点P、Q的定义知
=xy,由点P、Q的定义知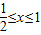 ,
,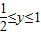 ,
,且
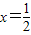 时,y=1;x=1时,
时,y=1;x=1时, .此时,均有
.此时,均有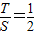 .
.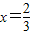 时,
时,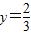 .此时,均有
.此时,均有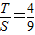 .得到
.得到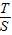 的范围为
的范围为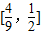 在根据(2)知
在根据(2)知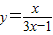 进行作差证明即可
进行作差证明即可解答:解:(1)
 =
=
(2)一方面,由(1),得
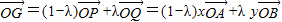 ;①
;①另一方面,∵G是△OAB的重心,
∴
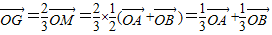 .②
.②而
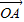 、
、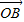 不共线,∴由①、②,
不共线,∴由①、②,得
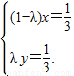
解之,得
 ,
,∴
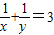 (定值).
(定值).(3)
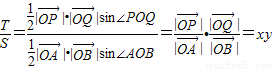 .
.由点P、Q的定义知
 ,
,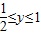 ,
,且
 时,y=1;x=1时,
时,y=1;x=1时,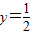 .
.此时,均有
 .
.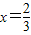 时,
时,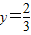 .
.此时,均有
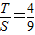 .
.以下证明:
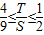 .
.由(2)知
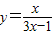 ,
,∵
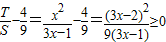 ,
,∴
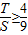 .
.∵
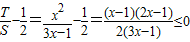 ,
,∴
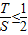 .
.∴
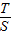 的取值范围
的取值范围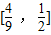 .
.点评:本题考查了向量的加减法,三角形的面积公式,作差法证明不等式,属于基础题.

练习册系列答案
相关题目
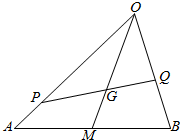 如图,G是△OAB的重心,P、Q分别是边OA、OB上的动点,且P、G、Q三点共线.
如图,G是△OAB的重心,P、Q分别是边OA、OB上的动点,且P、G、Q三点共线.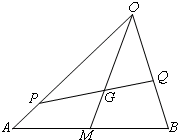 如图,G是△OAB的重心,P、Q分别是边OA、OB上的动点,且P、G、Q三点共线.
如图,G是△OAB的重心,P、Q分别是边OA、OB上的动点,且P、G、Q三点共线. 如图,G是△OAB的重心,P、Q分别是边OA、OB上的动点,且P、G、Q三点共线.
如图,G是△OAB的重心,P、Q分别是边OA、OB上的动点,且P、G、Q三点共线.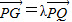 ,将
,将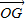 用λ、
用λ、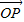 、
、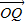 表示;
表示;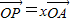 ,
,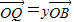 ,证明:
,证明: 是定值;
是定值;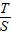 的取值范围.
的取值范围.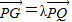 ,将
,将 用λ、
用λ、 、
、 表示;
表示;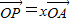 ,
,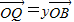 ,证明:
,证明: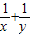 是定值.
是定值.