题目内容
x>0,y>0,且
+
=4,若x+2y≥m2-2m-6恒成立,则m范围是
| 2 |
| x |
| 1 |
| y |
-2≤m≤4
-2≤m≤4
.分析:先把x+2y转会为(x+2y)(
+
)×
展开后利用基本不等式求得其最小值,然后根据x+2y≥m2-2m-6求得m2-2m-6≤2,进而求得m的范围.
| 2 |
| x |
| 1 |
| y |
| 1 |
| 4 |
解答:解:∵∴x+2y=(x+2y)(
+
)×
=
(4+4×
+
)≥
(4+2×2)=2,
当且仅当4×
=
时取等号,
∵x+2y≥m2-2m-6恒成立,
∴m2-2m-6≤2,求得-2≤m≤4,
故答案为:-2≤m≤4.
| 2 |
| x |
| 1 |
| y |
| 1 |
| 4 |
| 1 |
| 4 |
| y |
| x |
| x |
| y |
| 1 |
| 4 |
当且仅当4×
| y |
| x |
| x |
| y |
∵x+2y≥m2-2m-6恒成立,
∴m2-2m-6≤2,求得-2≤m≤4,
故答案为:-2≤m≤4.
点评:本题主要考查了基本不等式在最值问题中的应用、函数恒成立问题.考查了学生分析问题和解决问题的能力.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
已知x>0,y>0,且
+
=1,若x+2y>m2+2m恒成立,则实数m的取值范围( )
| 2 |
| x |
| 1 |
| y |
| A、m≥4或m≤-2 |
| B、m≥2或m≤-4 |
| C、-4<m<2 |
| D、-2<m<4 |
若x>0,y>0,且2x+y=2,则
+
的最小值是( )
| 1 |
| x |
| 1 |
| y |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
已知x>0,y>0,且2x、a、b、3y成等差数列,3x、c、d、2y成等比数列,则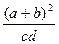 的最小值为( )
的最小值为( )
A.2 | B.2 | C.4 | D.4 |
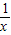 +
+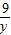 =2,求x+y的最小值.
=2,求x+y的最小值.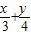 =1,求xy的最大值.
=1,求xy的最大值.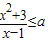 恒成立,求a的取值范围.
恒成立,求a的取值范围.