题目内容
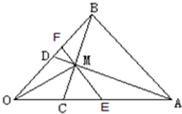
 如图,在△OAB中,延长BA到C,使AC=BA,在OB上取点D,使DB=
如图,在△OAB中,延长BA到C,使AC=BA,在OB上取点D,使DB= OB,DC与OA交于E,设
OB,DC与OA交于E,设 =
= ,
, =
= ,用
,用 ,
, 表示向量
表示向量 ,
, ,
, .
.
解:因为A是BC的中点,所以 =
= (
(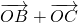 ),∴
),∴ =2
=2 -
- =2
=2 -
- .
. 
∴ =
= =2
=2 -
- -
-
 =2
=2 -
-
 .
.
由于D、E、C三点共线,
∴ =λ•
=λ• =λ(2
=λ(2 -
-
 )=2λ
)=2λ +
+
 .
.
由于 =
= +
+ =-
=-
 +μ
+μ =-
=-
 +μ
+μ .
.
∴2λ +
+
 =-
=-
 +μ
+μ ,故有 2λ=μ,
,故有 2λ=μ, λ=-
λ=- .
.
解得 λ= ,μ=
,μ= .
.
∴ =
=
 -
-
 .
.
分析:由 =
= (
(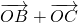 )求出
)求出 ;根据
;根据 =
= 求得结果;由于D、E、C三点共线,可得
求得结果;由于D、E、C三点共线,可得  =λ•
=λ• =2λ
=2λ +
+
 ,再由
,再由 =
= +
+ =-
=-
 +μ
+μ ,故有2λ
,故有2λ +
+
 =-
=-
 +μ
+μ ,解出λ和μ的值,即可求得
,解出λ和μ的值,即可求得 .
.
点评:本题考查平面向量基本定理及向量的表示,两个向量共线的性质,两个向量坐标形式的运算,属于中档题.
 =
= (
(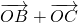 ),∴
),∴ =2
=2 -
- =2
=2 -
- .
. 
∴
 =
= =2
=2 -
- -
-
 =2
=2 -
-
 .
.由于D、E、C三点共线,
∴
 =λ•
=λ• =λ(2
=λ(2 -
-
 )=2λ
)=2λ +
+
 .
.由于
 =
= +
+ =-
=-
 +μ
+μ =-
=-
 +μ
+μ .
.∴2λ
 +
+
 =-
=-
 +μ
+μ ,故有 2λ=μ,
,故有 2λ=μ, λ=-
λ=- .
.解得 λ=
 ,μ=
,μ= .
.∴
 =
=
 -
-
 .
.分析:由
 =
= (
(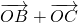 )求出
)求出 ;根据
;根据 =
= 求得结果;由于D、E、C三点共线,可得
求得结果;由于D、E、C三点共线,可得  =λ•
=λ• =2λ
=2λ +
+
 ,再由
,再由 =
= +
+ =-
=-
 +μ
+μ ,故有2λ
,故有2λ +
+
 =-
=-
 +μ
+μ ,解出λ和μ的值,即可求得
,解出λ和μ的值,即可求得 .
.点评:本题考查平面向量基本定理及向量的表示,两个向量共线的性质,两个向量坐标形式的运算,属于中档题.

练习册系列答案
相关题目
 如图,在△OAB中,
如图,在△OAB中, (2013•杭州二模)如图,在△OAB中,C为OA上的一点,且
(2013•杭州二模)如图,在△OAB中,C为OA上的一点,且 如图,在△OAB中,已知
如图,在△OAB中,已知 如图,在△OAB中,延长BA到C,使AC=BA,在OB上取点D,使DB=
如图,在△OAB中,延长BA到C,使AC=BA,在OB上取点D,使DB= 如图,在△OAB中,已知P为线段AB上的一点,且|
如图,在△OAB中,已知P为线段AB上的一点,且|