Question

（2013•杭州二模）如图，在△OAB中，C为OA上的一点，且

OC

=

2

3

OA

，D是BC的中点，过点A的直线l∥OD，P是直线l上的任意点，若

OP

=λ1

OB

+λ2

OC

，则λ₁-λ₂=

-

3

2

．

Answer 1

分析：根据OD是△OBC的中线，得

OD

=

1

2

OB

+

1

2

OC

．由直线l∥OD，可得存在实数k使

AP

=k

OD

，再化简得到

OP

=

OA

+

AP

=

k

2

OB

+（

3

2

+

k

2

）

OC

，结合已知等式可得

k

2

=λ₁且

3

2

+

k

2

=λ₂，由此即可算出则λ₁-λ₂的值．

解答：解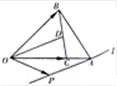：∵D是BC的中点，∴

OD

=

1

2

OB

+

1

2

OC

∵

OC

=

2

3

OA

，∴

OA

=

3

2

OC

∵直线l∥OD，∴存在实数k，使

AP

=k

OD

，
因此，

OP

=

OA

+

AP

=

3

2

OC

+k

OD

=

3

2

OC

+k（

1

2

OB

+

1

2

OC

）=

k

2

OB

+（

3

2

+

k

2

）

OC

，
∵由已知，得

OP

=λ1

OB

+λ2

OC

∴根据平面向量基本定理，得

k

2

=λ₁且

3

2

+

k

2

=λ₂
因此，λ₁-λ₂=

k

2

-（

3

2

+

k

2

）=-

3

2

故答案为：-

3

2

点评：本题在△OAB中，给出边的三等分点C和△OBC的中线OD，探索向量

OP

表示成

OB

、

OC

的线性组合问题，着重考查了平面向量的线性运算、平面向量的基本定理及其意义等知识，属于中档题．