题目内容
7.已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率e=$\frac{1}{2}$,且长轴长等于4.(Ⅰ)求椭圆C的方程;
(Ⅱ)F1,F2是椭圆C的两个焦点,⊙O是以F1,F2为直径的圆,直线l:y=kx+m与⊙O相切,并与椭圆C交于不同的两点A,B,若$\overrightarrow{OA}$•$\overrightarrow{OB}$=-$\frac{3}{2}$,求k的值.
分析 (I)由题意长轴长为4求得a的值,离心率e=$\frac{1}{2}$,得出c=1,可得b,即可求椭圆C的方程;
(II)由于圆O是以F1,F2为直径的圆,直线l:y=kx+m与⊙O相切,利用直线与圆相切的从要条件得到一个等式,把直线方程与椭圆方程联立利用整体代换的思想,根据$\overrightarrow{OA}$•$\overrightarrow{OB}$=-$\frac{3}{2}$,建立k的方程求k.
解答 解:(I)由题意,长轴长为4,即2a=4,解得:a=2,
∵离心率e=$\frac{1}{2}$,∴c=1,
∴b2=3,
∴椭圆的方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(II)由直线l与圆O相切,得:$\frac{|m|}{\sqrt{1+{k}^{2}}}$=1,∴m2=1+k2.
设A(x1,y1)B(x2,y2)
由直线l:y=kx+m与椭圆方程,消去y,
整理得:(3+4k2)x2+8kmx+4m2-12=0,
∴x1+x2=-$\frac{8km}{3+4{k}^{2}}$,x1x2=$\frac{4{m}^{2}-12}{3+4{k}^{2}}$,
∴y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=$\frac{3{m}^{2}-12{k}^{2}}{3+4{k}^{2}}$,
∴x1x2+y1y2=$\frac{7{m}^{2}-12{k}^{2}-12}{3+4{k}^{2}}$,
∵m2=1+k2,
∴x1x2+y1y2=$\frac{-5-5{k}^{2}}{3+4{k}^{2}}$=-$\frac{3}{2}$,
解得:k=±$\frac{\sqrt{2}}{2}$.
点评 此题考查了椭圆的基本性质及椭圆的标准方程,还考查了直线方程与椭圆方程联立之后的整体代换设而不求,还有求解问题时方程的思想.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{y^2}{4}$-$\frac{x^2}{5}$=1(y≤-2) | B. | $\frac{y^2}{4}$-$\frac{x^2}{5}$=1 | C. | $\frac{x^2}{4}$-$\frac{y^2}{5}$=1(x≤-2) | D. | $\frac{x^2}{4}$-$\frac{y^2}{5}$=1 |
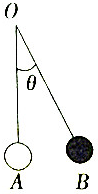 如图所示,一个单摆以OA为始边,OB为终边的角θ(-π<θ<π)与时间t(s)满足函数关系式θ=$\frac{1}{2}$sin(2t+$\frac{π}{2}$),则当t=0时,角θ的大小及单摆频率是( )
如图所示,一个单摆以OA为始边,OB为终边的角θ(-π<θ<π)与时间t(s)满足函数关系式θ=$\frac{1}{2}$sin(2t+$\frac{π}{2}$),则当t=0时,角θ的大小及单摆频率是( )| A. | $\frac{1}{2}$,$\frac{1}{π}$ | B. | 2,$\frac{1}{π}$ | C. | $\frac{1}{2}$,π | D. | 2,π |
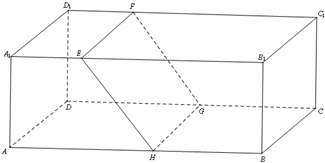 如图,在长方体ABCD-A1B1C1D1中,AB=16,AA1=8,BC=10,点E,F 分别在A1B1C1D1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形EFGH.
如图,在长方体ABCD-A1B1C1D1中,AB=16,AA1=8,BC=10,点E,F 分别在A1B1C1D1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形EFGH.