题目内容
15.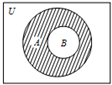 设全集U=R,集合A、B满足如图所示的关系,且A={x|x2-2x-3≤0},阴影部分表示的集合为{x|-1≤x<1},则集合B可以是( )
设全集U=R,集合A、B满足如图所示的关系,且A={x|x2-2x-3≤0},阴影部分表示的集合为{x|-1≤x<1},则集合B可以是( )| A. | {x|1<x<3} | B. | {x|1<x≤3} | C. | {x|1≤x<3} | D. | {x|1≤x≤3} |
分析 求出阴影部分对应的结合,结合集合的基本运算进行求解即可.
解答 解:阴影部分为集合A∩∁UB,
A={x|x2-2x-3≤0}={x|-1≤x≤3},
若B={x|1<x<3},则∁UB={x|x≥3或x≤1},则A∩∁UB={x|-1≤x≤1或x=3},不满足条件.
若B={x|1<x≤3},则∁UB={x|x>3或x≤1},则A∩∁UB={x|-1≤x≤1},不满足条件.
若B={x|1≤x<3},则∁UB={x|x≥3或x<1},则A∩∁UB={x|-1≤x<1或x=3},不满足条件.
若B={x|1≤x≤3},则∁UB={x|x>3或x<1},则A∩∁UB={x|-1≤x<1},满足条件.
故选:D.
点评 本题主要考查集合的基本运算,根据Venn图表示集合关系是解决本题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
6.下列说法中,正确的是( )
| A. | 命题“若am2<bm2,则a<b”的逆命题是真命题 | |
| B. | 命题“存在x∈R,x2-x>0”的否定是:“任意x∈R,x2-x≤0” | |
| C. | 命题“p或q”为真命题,则命题“p”和命题“q”均为真命题 | |
| D. | 已知x∈R,则“x>1”是“x>2”的充分不必要条件 |
20.从某班成员分别为3人、3人和4人的三个学习小组中选派4人组成一个环保宣传小组,则每个学习小组都至少有1人的选派方法种数是( )
| A. | 130 | B. | 128 | C. | 126 | D. | 124 |
7.定积分${∫}_{1}^{e}$($\frac{1}{x}$+2)dx的值为( )
| A. | 2e+1 | B. | 2e-1 | C. | e-2 | D. | 2e-2 |