题目内容
13.设变量x,y满足约束条件$\left\{\begin{array}{l}{x-y+2≤0}\\{x+y-7≤0}\\{x≥1}\end{array}\right.$,则$\frac{y}{x}$的最大值为6.分析 由约束条件作差可行域,利用$\frac{y}{x}$的几何意义,即可行域内的动点与原点连线的斜率,求其最大值得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{x-y+2≤0}\\{x+y-7≤0}\\{x≥1}\end{array}\right.$作差可行域如图,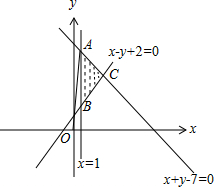
联立$\left\{\begin{array}{l}{x=1}\\{x+y-7=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=6}\end{array}\right.$,
∴A(1,6),
$\frac{y}{x}$的几何意义为可行域内的动点与原点连线的斜率,
由图可知,当动点为A时,可行域内的动点与原点连线的斜率最大,最大值为$\frac{6-0}{1-0}=6$.
故答案为:6.
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
4.已知p:|x|<2;q:x2-x-2<0,则p是q的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
1.函数f(x)的图象如图所示,下列数值排序正确的是( )


| A. | 0<f(3)-f(2)<f′(2)<f′(3) | B. | 0<f′(2)<f′(3)<f(3)-f(2) | C. | 0<f′(3)<f(3)-f(2)<f′(2) | D. | 0<f′(3)<f′(2)<f(3)-f(2) |
8.若△ABC中,cosA=$\frac{5}{13}$,cosB=$\frac{4}{5}$,则cosC的值为( )
| A. | $\frac{56}{65}$ | B. | -$\frac{56}{65}$ | C. | -$\frac{16}{65}$ | D. | $\frac{16}{65}$ |
18.设i是虚数单位,复数z=$\frac{2i}{1+i}$,则|z|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
5.在某次联考数学测试中,学生成绩ξ服从正态分布(100,σ2),(σ>0),若ξ在(80,120)内的概率为0.8,则落在(0,80)内的概率为( )
| A. | 0.05 | B. | 0.1 | C. | 0.15 | D. | 0.2 |
2.复数$\frac{3+i}{1-3i}$=( )
| A. | -i | B. | i | C. | 2i | D. | -2i |
3.已知sin($\frac{π}{6}-α$)=$\frac{3}{5}$,则sin($\frac{π}{6}+2α$)=( )
| A. | $\frac{4}{5}$ | B. | $\frac{7}{25}$ | C. | $\frac{9}{25}$ | D. | $\frac{16}{25}$ |
 如图,在边长为1的正六边形ABCDEF中,其中心为点O.
如图,在边长为1的正六边形ABCDEF中,其中心为点O.