题目内容
3.已知sin($\frac{π}{6}-α$)=$\frac{3}{5}$,则sin($\frac{π}{6}+2α$)=( )| A. | $\frac{4}{5}$ | B. | $\frac{7}{25}$ | C. | $\frac{9}{25}$ | D. | $\frac{16}{25}$ |
分析 由题意和二倍角公式可得cos($\frac{π}{3}$-2α)的值,再由整体思想和诱导公式可得sin($\frac{π}{6}+2α$)=cos($\frac{π}{3}$-2α),代值可得.
解答 解:∵sin($\frac{π}{6}-α$)=$\frac{3}{5}$,
∴cos($\frac{π}{3}$-2α)=1-2sin2($\frac{π}{6}-α$)=$\frac{7}{25}$,
∴sin($\frac{π}{6}+2α$)=sin[$\frac{π}{2}$-($\frac{π}{3}$-2α)]
=cos($\frac{π}{3}$-2α)=$\frac{7}{25}$,
故选:B.
点评 本题考查二倍角公式和诱导公式,涉及整体的思想,属中档题.

练习册系列答案
相关题目
11.若函数f(x)=$\frac{1}{a{x}^{2}+bx+c}$的部分图象如图所示,则abc=( )


| A. | 12 | B. | -12 | C. | 8 | D. | -8 |
18.复数z=(3-2i)i,则z-2$\overline{z}$=( )
| A. | -2-9i | B. | -2+9i | C. | 2-9i | D. | 2+9i |
 如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N. .
. 时,求函数
时,求函数 的最大值;
的最大值; 与
与 轴交于两点
轴交于两点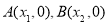 且
且 ,证明:
,证明: .
.