题目内容
(16分)
已知数列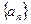 中,
中,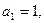 且点
且点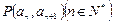 在直线
在直线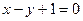 上.
上.
(1)求数列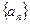 的通项公式;
的通项公式;
(2)若函数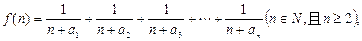
求函数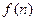 的最小值;
的最小值;
(3)设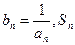 表示数列
表示数列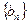 的前
的前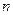 项和.试问:是否存在关于
项和.试问:是否存在关于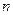 的整式
的整式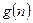 ,使得
,使得
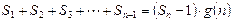 对于一切不小于2的自然数
对于一切不小于2的自然数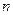 恒成立? 若存在,写出
恒成立? 若存在,写出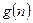 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。
已知数列
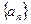 中,
中,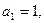 且点
且点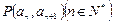 在直线
在直线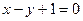 上.
上.(1)求数列
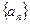 的通项公式;
的通项公式;(2)若函数
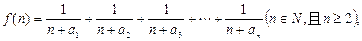
求函数
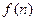 的最小值;
的最小值;(3)设
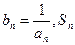 表示数列
表示数列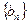 的前
的前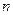 项和.试问:是否存在关于
项和.试问:是否存在关于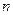 的整式
的整式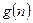 ,使得
,使得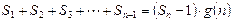 对于一切不小于2的自然数
对于一切不小于2的自然数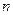 恒成立? 若存在,写出
恒成立? 若存在,写出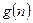 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。 (1)
(2)
(3)
解:(1)点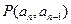 在直线x-y+1=0上,
在直线x-y+1=0上,
即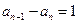
 ………………………………………2分
………………………………………2分
且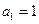 ,数列{
,数列{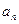 }是以1为首项,1为公差的等差数列
}是以1为首项,1为公差的等差数列
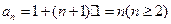 ,
,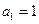 同样满足,所以
同样满足,所以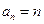 ……4分
……4分
(2)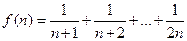
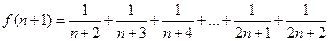 ……6分
……6分
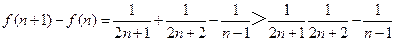
所以f(x)是单调递增,故f(n)的最小值是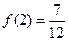 ……10分
……10分
(3)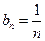 ,可得
,可得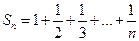 ,
,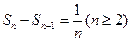 ……12分
……12分
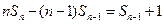
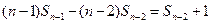
……
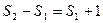
相加得: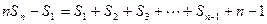
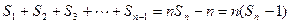 ,n≥2------------------15分
,n≥2------------------15分
所以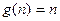
故存在关于n的整式g(x)=n,使得对于一切不小于2的自然数n恒成立。----16分
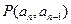 在直线x-y+1=0上,
在直线x-y+1=0上,即
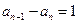
 ………………………………………2分
………………………………………2分且
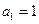 ,数列{
,数列{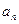 }是以1为首项,1为公差的等差数列
}是以1为首项,1为公差的等差数列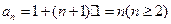 ,
,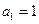 同样满足,所以
同样满足,所以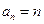 ……4分
……4分(2)
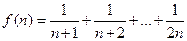
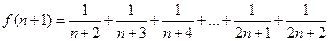 ……6分
……6分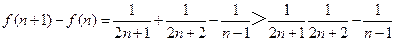
所以f(x)是单调递增,故f(n)的最小值是
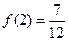 ……10分
……10分(3)
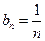 ,可得
,可得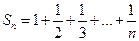 ,
,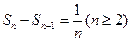 ……12分
……12分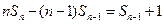
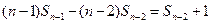
……
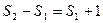
相加得:
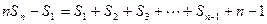
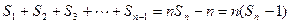 ,n≥2------------------15分
,n≥2------------------15分所以
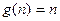
故存在关于n的整式g(x)=n,使得对于一切不小于2的自然数n恒成立。----16分

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
 N*),满足条件:
N*),满足条件: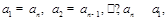 即
即 ,我们称其为“对称数列”.例如:数列1,2,3,4,3,2,1就是“对称数列”.已知数列
,我们称其为“对称数列”.例如:数列1,2,3,4,3,2,1就是“对称数列”.已知数列 是项数为不超过
是项数为不超过 的“对称数列”,并使得1,2,22,…,
的“对称数列”,并使得1,2,22,…, 依次为该数列中前连续的
依次为该数列中前连续的 项,则数列
项,则数列 可以是:
可以是: ①
① ;②
;② ; ③
; ③ ;④
;④ .
.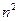 个数排成
个数排成 行
行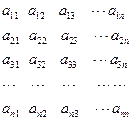
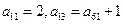 ,该数列第一列的
,该数列第一列的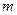 为公差的等差数列,每一行的
为公差的等差数列,每一行的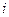 行第1列的数
行第1列的数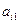 及第
及第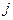 列的数
列的数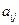
 为数列
为数列 的前n项和,且对任意
的前n项和,且对任意 都有
都有 ,记
,记
 ;
; 与
与 的大小;
的大小; 。
。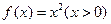 的图像上依次取点列
的图像上依次取点列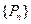 满足:
满足: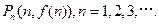 设
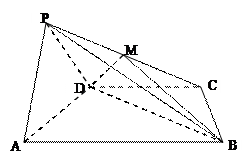
设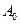 为平面上任意一点,若
为平面上任意一点,若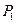 的对称点为
的对称点为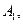
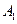 关于
关于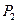 的对称点为
的对称点为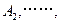 依次类推,可在平面上得相应点列
依次类推,可在平面上得相应点列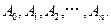 则当
则当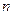 为偶数时,向量
为偶数时,向量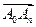 的坐标为_______________________.
的坐标为_______________________.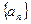 中,
中,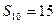 则
则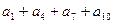 =( )
=( ) ”,这个符号表示若干个数相乘,例如:可将1×2×3×…×n记作
”,这个符号表示若干个数相乘,例如:可将1×2×3×…×n记作 ,
, ,其中
,其中 为数列
为数列 中的第
中的第 项.若
项.若 ________.
________. 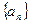 的前
的前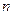 项和为
项和为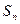 ,且
,且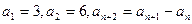 ,则
,则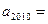 ( )
( )