题目内容
已知椭圆C: 的离心率与等轴双曲线的离心率互为倒数,直线
的离心率与等轴双曲线的离心率互为倒数,直线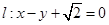 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切。
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切。
(Ⅰ)求椭圆C的方程;
(Ⅱ)设M是椭圆的上顶点,过点M分别作直线MA,MB交椭圆于A,B两点,设两直线的斜率分别为k1,k2,且k1+k2=2,证明:直线AB过定点(―1,―1)
 的离心率与等轴双曲线的离心率互为倒数,直线
的离心率与等轴双曲线的离心率互为倒数,直线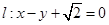 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切。
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切。(Ⅰ)求椭圆C的方程;
(Ⅱ)设M是椭圆的上顶点,过点M分别作直线MA,MB交椭圆于A,B两点,设两直线的斜率分别为k1,k2,且k1+k2=2,证明:直线AB过定点(―1,―1)
(Ⅰ) ;(Ⅱ)详见解析
;(Ⅱ)详见解析
 ;(Ⅱ)详见解析
;(Ⅱ)详见解析 试题分析:(I)由等轴双曲线的离心率为
 ,可得椭圆的离心率
,可得椭圆的离心率 ,因为直线
,因为直线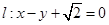 ,与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,利用点到直线的距离公式和直线与圆相切的性质可得,
,与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,利用点到直线的距离公式和直线与圆相切的性质可得, ,再利用
,再利用 即可得出;(II)分直线AB的斜率不存在与存在两种情况讨论,①不存在时比较简单;②斜率存在时,设直线AB的方程为
即可得出;(II)分直线AB的斜率不存在与存在两种情况讨论,①不存在时比较简单;②斜率存在时,设直线AB的方程为 ,由椭圆
,由椭圆 与椭圆的方程联立,利用根与系数的关系及斜率公式,再利用
与椭圆的方程联立,利用根与系数的关系及斜率公式,再利用 即可证明
即可证明 试题解析:(Ⅰ)由题意得
 ,
, 2分
2分即
 ,解得
,解得 4分
4分故椭圆C的方程为
 5分
5分(Ⅱ)当直线AB的斜率不存在时,设A
 ,则B
,则B ,由k1+k2=2得
,由k1+k2=2得 ,得
,得 7分
7分当直线AB的斜率存在时,设AB的方程为y=kx+b(
 ),
), ,
,
得
 ,
, 9分
9分

即

由
 ,
,
 11分
11分即

故直线AB过定点(―1,―1) 13分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
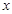 轴、
轴、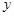 轴上滑动,且
轴上滑动,且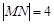 ,点P在线段MN上,满足
,点P在线段MN上,满足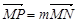
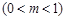 ,记点P的轨迹为曲线W.
,记点P的轨迹为曲线W.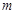 的值的关系;
的值的关系;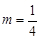 时,设A、B是曲线W与
时,设A、B是曲线W与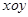 中,已知抛物线
中,已知抛物线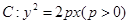 ,设点
,设点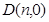 ,
,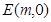 ,
,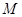 为抛物线
为抛物线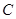 上的动点(异于顶点),连结
上的动点(异于顶点),连结 并延长交抛物线
并延长交抛物线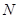 ,连结
,连结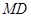 、
、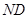 并分别延长交抛物线
并分别延长交抛物线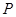 、
、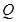 ,连结
,连结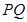 ,设
,设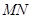 、
、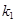 、
、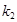 .
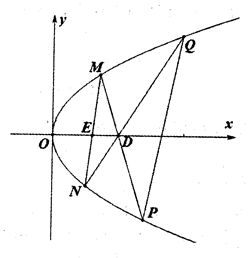
.
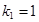 ,
,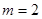 ,
,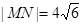 ,求
,求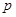 ;
;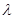 ,是的
,是的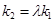 恒成立,若存在,请将
恒成立,若存在,请将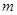 、
、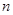 表示出来;若不存在请说明理由.
表示出来;若不存在请说明理由.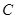 过定点
过定点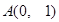 ,圆心
,圆心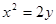 上,
上,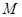 、
、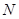 为圆
为圆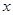 轴的交点.
轴的交点.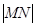 是否为一定值?请证明你的结论.
是否为一定值?请证明你的结论.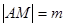 ,
,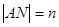 ,求
,求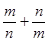 的最大值,并求出此时圆
的最大值,并求出此时圆 :
: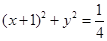 ,
, :
: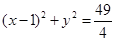 .动点P与
.动点P与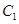 的方程;
的方程;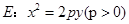 ,直线
,直线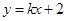 与E交于A、B两点,且
与E交于A、B两点,且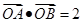 ,其中O为原点.
,其中O为原点.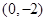 ,记直线CA、CB的斜率分别为
,记直线CA、CB的斜率分别为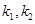 ,证明:
,证明: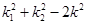 为定值.
为定值.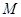 :
: 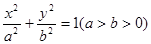 的离心率为
的离心率为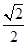 ,点
,点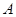 (
(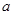 ,0),
,0),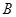 (0,
(0,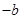 )原点
)原点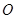 到直线
到直线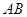 的距离为
的距离为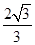 。
。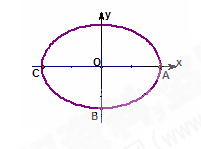
 为(
为(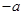 ,0),点
,0),点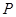 在椭圆
在椭圆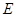 在直线
在直线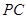 上,若直线
上,若直线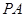 的方程为
的方程为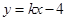 ,且
,且 ,试求直线
,试求直线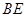 的方程.
的方程.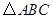 的顶点
的顶点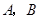 在椭圆
在椭圆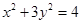 上,
上,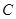 在直线
在直线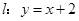 上,且
上,且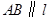 .
.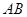 边通过坐标原点
边通过坐标原点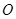 时,求
时,求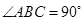 ,且斜边
,且斜边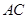 的长最大时,求
的长最大时,求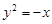 的焦点
的焦点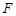 的直线交抛物线于
的直线交抛物线于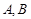 两点,且
两点,且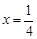 上的射影分别是
上的射影分别是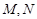 ,则
,则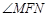 的大小为 .
的大小为 .