题目内容
9.若$\frac{2}{x}$+$\frac{1}{2y}$=1(x、y位正实数),则x+y的最小值是( )| A. | 5 | B. | $\frac{9}{2}$ | C. | 2 | D. | 1 |
分析 根据$\frac{2}{x}$+$\frac{1}{2y}$=1可得x+y=(x+y)($\frac{2}{x}$+$\frac{1}{2y}$),然后展开,利用基本不等式可求出最值,注意等号成立的条件.
解答 解:∵两个正实数x,y满足$\frac{2}{x}$+$\frac{1}{2y}$=1,
∴x+y=(x+y)($\frac{2}{x}$+$\frac{1}{2y}$)=2+$\frac{1}{2}$+$\frac{2y}{x}$+$\frac{x}{2y}$≥$\frac{5}{2}$+2$\sqrt{\frac{2y}{x}•\frac{x}{2y}}$=$\frac{9}{2}$,当且仅当$\frac{2y}{x}=\frac{x}{2y}$时取等号即x=3,y=$\frac{3}{2}$,
故x+y的最小值是$\frac{9}{2}$.
故选:B.
点评 本题主要考查了基本不等式的应用,解题的关键是“1”的活用,同时考查了运算求解的能力,属于基础题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
19.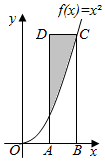 如图,点A的坐标为(1,0),点C的坐标为(2,4),函数f(x)=x2,四边形ABCD是矩形,则阴影区域的面积等于( )
如图,点A的坐标为(1,0),点C的坐标为(2,4),函数f(x)=x2,四边形ABCD是矩形,则阴影区域的面积等于( )
 如图,点A的坐标为(1,0),点C的坐标为(2,4),函数f(x)=x2,四边形ABCD是矩形,则阴影区域的面积等于( )
如图,点A的坐标为(1,0),点C的坐标为(2,4),函数f(x)=x2,四边形ABCD是矩形,则阴影区域的面积等于( )| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | 2 | D. | $\frac{7}{3}$ |
14.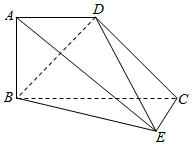 如图所示的几何体中,四边形ABCD为梯形,AD∥BC,AB⊥平面BEC,EC⊥CB.已知BC=2AD=2AB=2.
如图所示的几何体中,四边形ABCD为梯形,AD∥BC,AB⊥平面BEC,EC⊥CB.已知BC=2AD=2AB=2.
(I)证明:BD⊥平面DEC;
(Ⅱ)若EC=1,求AD与面BED所成角的正弦值.
 如图所示的几何体中,四边形ABCD为梯形,AD∥BC,AB⊥平面BEC,EC⊥CB.已知BC=2AD=2AB=2.
如图所示的几何体中,四边形ABCD为梯形,AD∥BC,AB⊥平面BEC,EC⊥CB.已知BC=2AD=2AB=2.(I)证明:BD⊥平面DEC;
(Ⅱ)若EC=1,求AD与面BED所成角的正弦值.
19.在平面直角坐标系xOy中,设锐角α的终边与圆O:x2+y2=1交于点M(x1,y1),点M沿圆O逆时针移动$\frac{π}{3}$个单位弧长后到达点N,设点N的坐标为(x2,y2),则x1•x2的取值范围是( )
| A. | (0,$\frac{\sqrt{3}}{2}$) | B. | (-$\frac{1}{4}$,$\frac{1}{2}$] | C. | [$\frac{1}{2}$,1] | D. | [-$\frac{1}{4}$,$\frac{1}{2}$) |
 如图,三棱锥P-ABC中,△ABC是正三角形,PC⊥平面ABC,PC=AC=2,E为AC中点,EF⊥AP,垂足为F.
如图,三棱锥P-ABC中,△ABC是正三角形,PC⊥平面ABC,PC=AC=2,E为AC中点,EF⊥AP,垂足为F.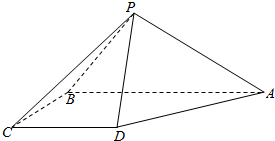 如图,四棱锥P-ABCD中,平面PAB⊥平面ABCD,底面ABCD为直角梯形,AB=2CD=2BC=2,AB∥CD,AB⊥BC,△PAB为等腰直角三角形且PA⊥PB.
如图,四棱锥P-ABCD中,平面PAB⊥平面ABCD,底面ABCD为直角梯形,AB=2CD=2BC=2,AB∥CD,AB⊥BC,△PAB为等腰直角三角形且PA⊥PB.