题目内容
已知：
=
+λ(
+
)，λ∈（0，+∞），则点P的轨迹一定经过△ABC的（ ）
| OP |
| OA |
| ||
|A
|
| ||
|A
|
| A、内心 | B、外心 | C、垂心 | D、重心 |
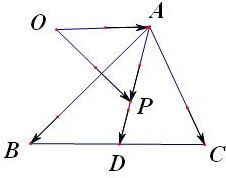
分析：法一：作出如图的三角形AD⊥BC，可以得出 |
|sinB=|
|sinC=AD，由此对已知条件变形即可得出结论；
法二：将 |
|sinB=|
|sinC提取出来，转化成λt（
+
），而λt（
+
）表示与
共线的向量，点D是BC的中点，故P的轨迹一定通过三角形的重心．
| AB |
| AC |
法二：将 |
| AB |
| AC |
| AB |
| AC |
| AB |
| AC |
| AD |
解答：
解：法一：作出如图的图形AD⊥BC，由于 |
|sinB=|
|sinC=AD，
∴
=
+λ(
+
)=
+
(
+
)
由加法法则知，P在三角形的中线上
故动点P的轨迹一定通过△ABC的重心；
法二：
∵|
|sinB=|
|sinC设它们等于
∴
=
+λt（
+
）
而
+
=2
λt（
+
）表示与
共线的向量
而点D是BC的中点，所以即P的轨迹一定通过三角形的重心．
故选D．
解：法一：作出如图的图形AD⊥BC，由于 || AB |
| AC |
∴
| OP |
| OA |
| ||
|
|
| ||
|
|
| OA |
| λ |
| |AD| |
| AB |
| AC |
由加法法则知，P在三角形的中线上
故动点P的轨迹一定通过△ABC的重心；
法二：
∵|
| AB |
| AC |
| 1 |
| t |
∴| OP |
| OA |
| AB |
| AC |
而
| AB |
| AC |
| AD |
λt（
| AB |
| AC |
| AD |
| AP |
而点D是BC的中点，所以即P的轨迹一定通过三角形的重心．
故选D．
点评：本题考点是三角形的五心，考查了五心中重心的几何特征以及向量的加法与数乘运算，解答本题的关键是理解向量加法的几何意义，从而确定点的几何位置．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目