题目内容
已知函数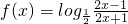 (x∈(-∞,
(x∈(-∞,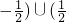 ,(
,( ,+∞)).
,+∞)).
(1)判断函数f(x)的奇偶性,并说明理由;
(2)指出函数f(x)在区间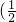 ,+∞)上的单调性,并加以证明.
,+∞)上的单调性,并加以证明.
解:(1)∵函数的定义域(-∞,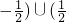 ∪(
∪( ,+∞)关于原点对称.
,+∞)关于原点对称.
且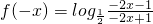 =
= =
=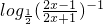 =-f(x),
=-f(x),
所以函数f(x)是奇函数.
(2)设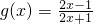 =
=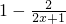 .设-m<x1<x2,则g(x1)-g(x2)=
.设-m<x1<x2,则g(x1)-g(x2)=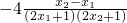 ,
,
因为m<0,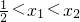 ,所以x2-x1>0,2x1+1>0,2x2+1>0,
,所以x2-x1>0,2x1+1>0,2x2+1>0,
所以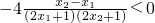 ,即g(x1)<g(x2),
,即g(x1)<g(x2),
因为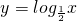 是减函数,所以
是减函数,所以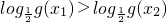 ,即f(x1)>f(x2),
,即f(x1)>f(x2),
所以f(x)在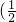 ,+∞)上是减函数.
,+∞)上是减函数.
分析:(1)根据奇偶性的定义,判断f(-x)与f(x)之间的关系,即可判断函数f(x)的奇偶性;
(2)利用原始的定义进行证明,在区间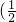 ,+∞)上任取x1,x2且x1<x2,只要证f(x2)>f(x1)就可以可,把x1和x2分别代入函数f (x)进行证明.
,+∞)上任取x1,x2且x1<x2,只要证f(x2)>f(x1)就可以可,把x1和x2分别代入函数f (x)进行证明.
点评:此题主要考查多项式函数的定义域、奇偶性和单调性,解题的关键是利用定义进行证明,是一道基础题.
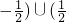 ∪(
∪( ,+∞)关于原点对称.
,+∞)关于原点对称.且
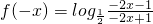 =
= =
=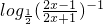 =-f(x),
=-f(x),所以函数f(x)是奇函数.
(2)设
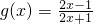 =
=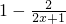 .设-m<x1<x2,则g(x1)-g(x2)=
.设-m<x1<x2,则g(x1)-g(x2)=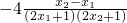 ,
,因为m<0,
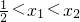 ,所以x2-x1>0,2x1+1>0,2x2+1>0,
,所以x2-x1>0,2x1+1>0,2x2+1>0,所以
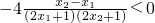 ,即g(x1)<g(x2),
,即g(x1)<g(x2),因为
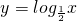 是减函数,所以
是减函数,所以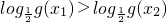 ,即f(x1)>f(x2),
,即f(x1)>f(x2),所以f(x)在
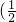 ,+∞)上是减函数.
,+∞)上是减函数.分析:(1)根据奇偶性的定义,判断f(-x)与f(x)之间的关系,即可判断函数f(x)的奇偶性;
(2)利用原始的定义进行证明,在区间
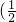 ,+∞)上任取x1,x2且x1<x2,只要证f(x2)>f(x1)就可以可,把x1和x2分别代入函数f (x)进行证明.
,+∞)上任取x1,x2且x1<x2,只要证f(x2)>f(x1)就可以可,把x1和x2分别代入函数f (x)进行证明.点评:此题主要考查多项式函数的定义域、奇偶性和单调性,解题的关键是利用定义进行证明,是一道基础题.

练习册系列答案
相关题目
已知函数f(x)=
,则它是( )
| ||
| |x-3|-3 |
| A、奇函数 | B、偶函数 |
| C、既奇又偶函数 | D、非奇非偶函数 |
已知函数f(x)=
则“-2≤a≤0”是“f(x)在R上单调递增”的( )
|
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |