题目内容
已知函数f(x)=ax3-
(a+2)x2+6x+b在x=2处取得极值.
(Ⅰ)求a的值及f(x)的单调区间;
(Ⅱ)若x∈[1,4]时,不等式f(x)>b2恒成立,求b的取值范围.
| 3 |
| 2 |
(Ⅰ)求a的值及f(x)的单调区间;
(Ⅱ)若x∈[1,4]时,不等式f(x)>b2恒成立,求b的取值范围.
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:计算题,函数的性质及应用,导数的综合应用
分析:(Ⅰ)求出导数,由题意得,f'(2)=0,求出a的值,再令导数大于0,得增区间,令导数小于0,得减区间;
(Ⅱ)x∈[1,4]时,不等式f(x)>b2恒成立即为f(x)的最小值大于b2,在[1,4]上恒成立,只要求出最小值即可.
(Ⅱ)x∈[1,4]时,不等式f(x)>b2恒成立即为f(x)的最小值大于b2,在[1,4]上恒成立,只要求出最小值即可.
解答:
解:(Ⅰ)∵函数f(x)=ax3-
(a+2)x2+6x+b,
∴f'(x)=3ax2-3(a+2)x+6,
∴f'(2)=12a-6a-12+6=0,
∴a=1.
由f'(x)=3x2-9x+6>0得x>2或x<1,
由f'(x)=3x2-9x+6<0得1<x<2,
∴函数f(x)的单调增区间为(-∞,1)、(2,+∞),单调减区间为(1,2).
(Ⅱ)f(x)=x3-
x2+6x+b,
当x∈[1,4]时,不等式f(x)>b2恒成立,即有f(x)的最小值大于b2,
∵f(x)min=f(2)=2+b,
∴2+b>b2,-1<b<2,
∴b的取值范围(-1,2).
| 3 |
| 2 |
∴f'(x)=3ax2-3(a+2)x+6,
∴f'(2)=12a-6a-12+6=0,
∴a=1.
由f'(x)=3x2-9x+6>0得x>2或x<1,
由f'(x)=3x2-9x+6<0得1<x<2,
∴函数f(x)的单调增区间为(-∞,1)、(2,+∞),单调减区间为(1,2).
(Ⅱ)f(x)=x3-
| 9 |
| 2 |
当x∈[1,4]时,不等式f(x)>b2恒成立,即有f(x)的最小值大于b2,
∵f(x)min=f(2)=2+b,
∴2+b>b2,-1<b<2,
∴b的取值范围(-1,2).
点评:本题考查导数的综合应用:求单调区间、求极值、求最值,考查不等式的恒成立问题转化为求函数的最值问题,属于中档题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
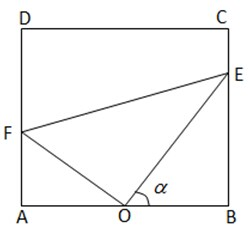 南海中学校园内建有一块矩形草坪ABCD,AB=50米,BC=25
南海中学校园内建有一块矩形草坪ABCD,AB=50米,BC=25 如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且|MD|=
如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且|MD|=