题目内容
已知命题P:函数f(x)=(2a-5)x是R上的减函数.命题Q:在x∈R时,不等式x2-ax+2>0恒成立.若命题“P∪Q”是真命题,求实数a的取值范围.
考点:复合命题的真假
专题:简易逻辑
分析:分别求出命题P,Q下的a的取值,根据P∪Q为真命题,分成P真Q真,P真Q假,P假Q真,这几种情况,求每种情况下的a的取值,然后求并集即可.
解答:
解:命题P:函数f(x)=(2a-5)x是R上的减函数;
∴0<2a-5<1;
∴
<a<3;
命题Q:在x∈R时,不等式x2-ax+2>0恒成立;
∴△=a2-8<0,解得-2
<a<2
;
∵P∪Q为真命题;
∴若P真Q真:
<a<2
;
若P真Q假:2
≤a<3;
若P假Q真:-2
<a≤
;
综上得a的取值范围为:(-2
,3).
∴0<2a-5<1;
∴
| 5 |
| 2 |
命题Q:在x∈R时,不等式x2-ax+2>0恒成立;
∴△=a2-8<0,解得-2
| 2 |
| 2 |
∵P∪Q为真命题;
∴若P真Q真:
| 5 |
| 2 |
| 2 |
若P真Q假:2
| 2 |
若P假Q真:-2
| 2 |
| 5 |
| 2 |
综上得a的取值范围为:(-2
| 2 |
点评:考查指数函数的单调性,一元二次不等式的解和判别式△的关系.

练习册系列答案
相关题目
若U={1,2,3,4,5,6,7,8},A={1,3,4},B={5,6,7},则(∁UA)∩(∁UB)=( )
| A、{2,8} |
| B、{2,6,8} |
| C、{1,3,5,7} |
| D、{1,2,3,5,6,7} |
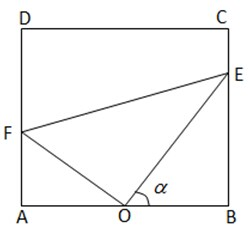 南海中学校园内建有一块矩形草坪ABCD,AB=50米,BC=25
南海中学校园内建有一块矩形草坪ABCD,AB=50米,BC=25