题目内容
某商场将进货单价为40元的商品按50元一个出售时,能卖出500个,已知这种商品每涨价一元,其销售量就减少10个,为得到最大利润,销售价应定为多少元?最大利润是多少元?
考点:根据实际问题选择函数类型
专题:应用题,函数的性质及应用
分析:设利润为y元,商品涨价x元/个,根据每涨价1元,其销售量就减少10个,可建立函数解析式,再利用配方法,即可求得最大利润.
解答:
解:设利润为y元,商品涨价x元/个,则
y=(500-10x)(50+x)-(500-10x)•40(x∈[0,50],x∈N*)
∴y=(500-10x)(10+x)=-10x2+400x+5000=-10(x-20)2+9000
∴当x=20时,y有最大值9000,即销售价应定为70元/个
答:销售单价定为70元时,最大总利润为9000元.
y=(500-10x)(50+x)-(500-10x)•40(x∈[0,50],x∈N*)
∴y=(500-10x)(10+x)=-10x2+400x+5000=-10(x-20)2+9000
∴当x=20时,y有最大值9000,即销售价应定为70元/个
答:销售单价定为70元时,最大总利润为9000元.
点评:本题考查函数模型的构建,考查利用配方法求函数的最值,确定二次函数是关键,属于中档题.

练习册系列答案
相关题目
函数f(x)=sinx•ln(x2+1)的部分图象可能是( )
A、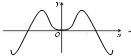 |
B、 |
C、 |
D、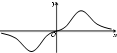 |
已知函数f(x)=3sinωx(ω>0)在区间[-
,
]上的最大值是3,则ω的最小值为( )
| π |
| 3 |
| π |
| 4 |
A、
| ||
B、
| ||
| C、2 | ||
| D、4 |