题目内容
3.已知双曲线$\frac{x^2}{9}-\frac{y^2}{27}=1$与点M(5,3),F为右焦点,若双曲线上有一点P,则$PM+\frac{1}{2}PF$的最小值为$\frac{7}{2}$.分析 由题意可知:双曲线的第二定义可知:$\frac{丨PF丨}{丨PN丨}$=e,可得丨PF丨=e丨PN丨=2丨PN丨,丨PN丨=$\frac{1}{2}$丨PF丨,丨PM丨+$\frac{1}{2}$丨PF丨=丨PM丨+丨PN丨,当且仅当M、N、P三点共线时丨PM丨+丨PN丨=丨MN丨时取最小值,代入求得P点坐标,即可求得丨PM丨+$\frac{1}{2}$丨PF丨的最小值为丨MN丨=$\frac{7}{2}$.
解答 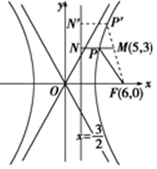 解:双曲线$\frac{x^2}{9}-\frac{y^2}{27}=1$,焦点在x轴上,a=3,b=3$\sqrt{3}$,c=$\sqrt{{a}^{2}+{b}^{2}}$=6,
解:双曲线$\frac{x^2}{9}-\frac{y^2}{27}=1$,焦点在x轴上,a=3,b=3$\sqrt{3}$,c=$\sqrt{{a}^{2}+{b}^{2}}$=6,
由双曲线离心率e=$\frac{c}{a}$=2,右准线为x=$\frac{{a}^{2}}{c}$=$\frac{3}{2}$,
作MN⊥l于N,交双曲线右支于P,连结FP,则
由双曲线的第二定义可知:$\frac{丨PF丨}{丨PN丨}$=e,可得丨PF丨=e丨PN丨=2丨PN丨,
∴丨PN丨=$\frac{1}{2}$丨PF丨,
因此丨PM丨+$\frac{1}{2}$丨PF丨=丨PM丨+丨PN丨,
当且仅当M、N、P三点共线时丨PM丨+丨PN丨=丨MN丨时取最小值,
此时,在双曲线$\frac{x^2}{9}-\frac{y^2}{27}=1$中,令y=3,解得:x=±2$\sqrt{3}$,
∴x>0,
∴取x=2$\sqrt{3}$,
即当P的坐标为(2$\sqrt{3}$,3)时丨PM丨+$\frac{1}{2}$丨PF丨的最小值为丨MN丨=$\frac{7}{2}$.
丨PM丨+$\frac{1}{2}$丨PF丨的最小值为$\frac{7}{2}$.
故答案为:$\frac{7}{2}$.
点评 本题考查双曲线的标准方程,直线与双曲线的位置关系,考查双曲线的第二定义的应用,考查计算能力,属于中档题

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案| A. | ?x<0,sinx≤0或tanx≤0 | B. | ?x<0,sinx≤0且tanx≤0 | ||
| C. | ?x≥0,sinx≤0或tanx≤0 | D. | ?x≥0,sinx≤0且tanx≤0 |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$或$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$或$\frac{\sqrt{3}}{2}$ |
| A. | (-1,2) | B. | (-2,-1] | C. | (-2,-1) | D. | (2,3) |
 已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<π)的部分图象如图所示,且$A({\frac{π}{2},1}),B({π,-1})$,则φ值为-$\frac{5π}{6}$.
已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<π)的部分图象如图所示,且$A({\frac{π}{2},1}),B({π,-1})$,则φ值为-$\frac{5π}{6}$.