题目内容
求证:(
)3≤
.a,b,c>0.
| a+b+c |
| 3 |
| a3+b3+c3 |
| 3 |
考点:不等式的证明
专题:证明题,不等式的解法及应用
分析:设函数f(x)=x3(x>0),则点P(
,f(
))在f(x)图象上,设过P的切线方程为:y=kx+t,由于x>0时,图象上凹,切线在图象的下方,则f(a)≥ka+t,f(b)≥kb+t,f(c)≥kc+t,累加即可得证.
| a+b+c |
| 3 |
| a+b+c |
| 3 |
解答:
解:设函数f(x)=x3(x>0),
则点P(
,f(
))在f(x)图象上,
设过P的切线方程为:y=kx+t,
由于x>0时,图象上凹,切线在图象的下方,
则f(a)≥ka+t,f(b)≥kb+t,f(c)≥kc+t,
则有
≥k•
+t,
由于f(
)=k•
+t,
则f(
)≤
,
即有(
)3≤
.
则点P(
| a+b+c |
| 3 |
| a+b+c |
| 3 |
设过P的切线方程为:y=kx+t,
由于x>0时,图象上凹,切线在图象的下方,
则f(a)≥ka+t,f(b)≥kb+t,f(c)≥kc+t,
则有
| f(a)+f(b)+f(c) |
| 3 |
| a+b+c |
| 3 |
由于f(
| a+b+c |
| 3 |
| a+b+c |
| 3 |
则f(
| a+b+c |
| 3 |
| f(a)+f(b)+f(c) |
| 3 |
即有(
| a+b+c |
| 3 |
| a3+b3+c3 |
| 3 |
点评:本题考查不等式的证明,考查运用图象与切线的关系证明不等式的方法,考查推理能力,属于中档题.

练习册系列答案
相关题目
如图:已知在?ABCD中,对角线AC交BD于O、E为DO的中点,AE交CD于F,设
=
,
=
,则
=( )

| AB |
| a |
| AD |
| b |
| BF |

A、-
| ||||||
B、-
| ||||||
C、
| ||||||
D、-
|
已知正实数a,b满足a+2b=1,则
的最小值为( )
| b+a |
| ab |
A、3+2
| ||
B、1+
| ||
| C、4 | ||
D、2
|
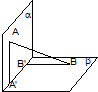 平面α⊥平面β,A∈α,B∈β,AB与两平面α、β所成的角分别为
平面α⊥平面β,A∈α,B∈β,AB与两平面α、β所成的角分别为