题目内容
8．设f（x）=$\frac{1}{3}$x3+3x2+ax，若g（x）=$\frac{1}{{4}^{x}}$，对任意x1∈[$\frac{1}{2}$，1]，存在x2∈[$\frac{1}{2}$，2]，使得f′（x1）≤g（x2）成立，则实数a的取值范围为（ ）| A． | [-$\frac{11}{4}$，+∞） | B． | （-∞，-$\frac{13}{2}$] | C． | （-∞，-$\frac{11}{4}$] | D． | [-$\frac{13}{2}$，+∞） |
分析 由题意，只要f'（x）max≤g（x）max，分别求出两个函数的最大值，转化为关于a 的不等式求a的范围．
解答 解：由题意，对任意x1∈[$\frac{1}{2}$，1]，存在x2∈[$\frac{1}{2}$，2]，
使得f'（x1）≤g（x2）成立，
所以f'（x）max≤g（x）max，f'（x）=x2+6x+a=（x+3）2+a-9，在[$\frac{1}{2}$，1]单调递增，
∴f'（x）max=f'（1）=7+a，g（x）在[$\frac{1}{2}$，2]单调递减，
则g（x）max=g（$\frac{1}{2}$）=$\frac{1}{2}$，所以7+a$≤\frac{1}{2}$，则a$≤\frac{1}{2}-7=-\frac{13}{2}$；
所以实数a的取值范围为（-$∞，-\frac{13}{2}$）；
故选B．
点评 本题考查了三次函数和指数函数的单调性以及存在与任意问题的解决办法；属于中档题．
练习册系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
9．定义：分子为1且分母为正整数的分数为单位分数，我们可以把1拆为若干个不同的单位分数之和．如：1=$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{6}$，1=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+$\frac{1}{12}$，1=$\frac{1}{2}$+$\frac{1}{5}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{20}$，以此类推，可得：1=$\frac{1}{2}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{30}$+$\frac{1}{42}$+$\frac{1}{56}$+$\frac{1}{72}$+$\frac{1}{90}$+$\frac{1}{110}$+$\frac{1}{132}$+$\frac{1}{156}$，其中a＜b，a，b∈N*，设1≤x≤a，1≤y≤b，则$\frac{x+y+4}{x+2}$的最小值为（ ）
| A． | $\frac{25}{3}$ | B． | $\frac{23}{7}$ | C． | $\frac{8}{7}$ | D． | $\frac{6}{5}$ |
6．某校高三共有男生400名，从所有高三男生中随机抽取20名男生测量身高（单位：cm）作为样本，得到频率分布表与频率分布直方图1（部分）如表：
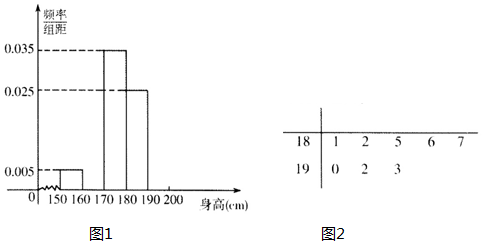
（Ⅰ）求n1、n2、f1、f2；
（Ⅱ）试估计身高不低于180cm的该校高三男生人数，并说明理由；
（Ⅲ）从样本中不低于180cm的男生身高，绘制成茎叶图（图2）；
现从身高不低于185cm的男生中任取3名参加选拔性测试，求至少有两位身高不低于190cm的概率．
| 分组 | 频数 | 频率 |
| [150，160） | 1 | |
| [160，170） | n1 | f1 |
| [170，180） | n2 | f2 |
| [180，190） | 5 | |
| [190，200] | 3 |
（Ⅰ）求n1、n2、f1、f2；
（Ⅱ）试估计身高不低于180cm的该校高三男生人数，并说明理由；
（Ⅲ）从样本中不低于180cm的男生身高，绘制成茎叶图（图2）；
现从身高不低于185cm的男生中任取3名参加选拔性测试，求至少有两位身高不低于190cm的概率．
