题目内容
已知n是正整数,若
+
<
,则n的取值范围是
| C | 2 n |
| C | 3 n |
| C | 4 n |
n≥9且n∈N+
n≥9且n∈N+
.分析:根据题意,由组合数的性质可将
+
<
变形为Cn+13<Cn4,由组合数公式将其展开可得
<
,整理变形可得n2-9n+2>0,解可得n的取值范围,结合n为正整数,综合可得答案.
| C | 2 n |
| C | 3 n |
| C | 4 n |
| (n+1)n(n-1) |
| 3×2×1 |
| n×(n-1)×(n-2)×(n-3) |
| 4×3×2×1 |
解答:解:根据题意,Cn2+Cn3=Cn+13,
则
+
<
⇒Cn+13<Cn4,
即
<
,
变形可得n2-9n+2>0;
解可得n>
或n<
,
又由n是正整数,
则n≥9且n∈N+,
故答案为n≥9且n∈N+.
则
| C | 2 n |
| C | 3 n |
| C | 4 n |
即
| (n+1)n(n-1) |
| 3×2×1 |
| n×(n-1)×(n-2)×(n-3) |
| 4×3×2×1 |
变形可得n2-9n+2>0;
解可得n>
9+
| ||
| 2 |
9-
| ||
| 2 |
又由n是正整数,
则n≥9且n∈N+,
故答案为n≥9且n∈N+.
点评:本题考查组合数公式的性质,注意牢记组合数公式与组合数公式的性质.

练习册系列答案
相关题目
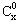 =1,这是组合数
=1,这是组合数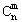 (n、m是正整数,且m≤n)的一种推广.
(n、m是正整数,且m≤n)的一种推广.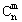 =C
=C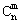 +C
+C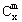 (x∈R,m是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
(x∈R,m是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.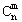 是正整数,证明:当x∈Z,m是正整数时,
是正整数,证明:当x∈Z,m是正整数时,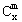 ∈Z
∈Z