题目内容

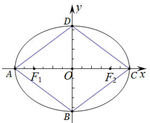精英家教网如图椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的四个顶点连成的菱形ABCD的面积为16
3
，直线AD的斜率为
3
2
．
（1）求椭圆的方程及左、右焦点F1、F2的坐标；
（2）双曲线
x2
u2
-
y2
v2
=1的渐近线分别与菱形的边平行，且以椭圆焦点F1、F2为焦点，
求双曲线的方程．
分析：（1）由菱形ABCD的面积及直线AD的斜率建立关于a，b的方程即可求得a，b的值，最后写出椭圆方程的焦点坐标即可；
（2）渐近线分别与菱形的边平行，且以椭圆焦点F1、F2为焦点，建立关于u，v的方程即可求得它们的值，最后写出双曲线方程即可；
解答：解：（1）由
b
a
=
3
2
及
1
2
(2a)(2b)=16
3
得，
a=4，b=2
3
；
椭圆方程为：
x2
16
+
y2
12
=1；　…（5分）
焦点为：F1（-2，0），F2（2，0）；…（7分）
（2）由
v
u
=
3
2
及u2+v2=4得：
u2=
16
7
，v2=
12
7
；
所以，双曲线的方程为：
7x2
16
-
7y2
12
=1．　　…（14分）
点评：本小题主要考查双曲线的标准方程、椭圆的简单性质等基础知识，考查运算求解能力，考查数形结合思想，属于基础题．
练习册系列答案
相关题目
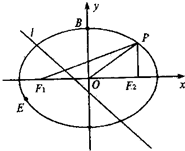精英家教网如图，已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的焦点和上顶点分别为F1、F2、B，我们称△F1BF2为椭圆C的特征三角形．如果两个椭圆的特征三角形是相似的，则称这两个椭圆是“相似椭圆”，且三角形的相似比即为椭圆的相似比．
（1）已知椭圆C1：
x2
4
+y2=1和C2：
x2
16
+
y2
4
=1，判断C2与C1是否相似，如果相似则求出C2与C1的相似比，若不相似请说明理由；
（2）已知直线l：y=x+1，在椭圆Cb上是否存在两点M、N关于直线l对称，若存在，则求出函数f（b）=|MN|的解析式．
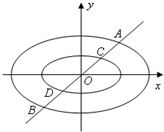精英家教网如图，已知椭圆C：
x2
a2
+
y2
2
=1(a＞
2
)的左右焦点分别为F1、F2，点B为椭圆与y轴的正半轴的交点，点P在第一象限内且在椭圆上，且PF2与x轴垂直，
F1P
•
OP
=5．
（1）求椭圆C的方程；
（2）设点B关于直线l：y=-x+n的对称点E（异于点B）在椭圆C上，求n的值．
精英家教网定义：由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”．如果两个椭圆的“特征三角形”是相似的，则称这两个椭圆是“相似椭圆”，并将三角形的相似比称为椭圆的相似比．已知椭圆C1：
x2
4
+y2=1．
（1）若椭圆C2：
x2
16
+
y2
4
=1，判断C2与C1是否相似？如果相似，求出C2与C1的相似比；如果不相似，请说明理由；
（2）写出与椭圆C1相似且短半轴长为b的椭圆Cb的方程；若在椭圆Cb上存在两点M、N关于直线y=x+1对称，求实数b的取值范围？
（3）如图：直线y=x与两个“相似椭圆”M：
x2
a2
+
y2
b2
=1和Mλ：
x2
a2
+
y2
b2
=λ2(a＞b＞0，0＜λ＜1)分别交于点A，B和点C，D，试在椭圆M和椭圆Mλ上分别作出点E和点F（非椭圆顶点），使△CDF和△ABE组成以λ为相似比的两个相似三角形，写出具体作法．（不必证明）
如图，已知椭圆C：
x2
a2
+
y2
b2
=1的离心率为
3
2
，过椭圆C上一点P（2，1）作倾斜角互补的两条直线，分别与椭圆交于点A、B，直线AB与x轴交于点M，与y轴负半轴交于点N．
（Ⅰ）求椭圆C的方程：
（Ⅱ）若S△PMN=
3
2
，求直线AB的方程．
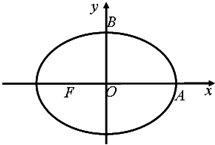精英家教网如图，点F是椭圆W：
x2
a2
+
y2
b2
=1(a＞b＞0)的左焦点，A、B分别是椭圆的右顶点与上顶点，椭圆的离心率为
1
2
，三角形ABF的面积为
3
3
2
，
（Ⅰ）求椭圆W的方程；
（Ⅱ）对于x轴上的点P（t，0），椭圆W上存在点Q，使得PQ⊥AQ，求实数t的取值范围；
（Ⅲ）直线l：y=kx+m（k≠0）与椭圆W交于不同的两点M、N （M、N异于椭圆的左右顶点），若以MN为直径的圆过椭圆W的右顶点A，求证：直线l过定点，并求出该定点的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网