Question

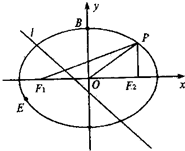如图，已知椭圆C：

x2

a2

+

y2

2

=1(a＞

2

)的左右焦点分别为F₁、F₂，点B为椭圆与y轴的正半轴的交点，点P在第一象限内且在椭圆上，且PF₂与x轴垂直，

F1P

•

OP

=5．
（1）求椭圆C的方程；
（2）设点B关于直线l：y=-x+n的对称点E（异于点B）在椭圆C上，求n的值．

Answer 1

分析：（1）根据椭圆的方程和PF₂与x轴垂直表示出F₁和P的坐标，利用F₁和P的坐标及原点O的坐标分别表示

F1P

和

OP

，然后利用平面向量的数量积的运算法则表示出

F1P

•

OP

，让其值等于5，列出关于a的方程，求出方程的解即可得到a的值，代入椭圆方程即可；
（2）根据椭圆方程求出B的坐标，设E和B关于直线l对称，则直线BE的斜率与直线l的斜率乘积为-1，根据直线l的斜率求出直线BE的斜率，根据B的坐标和求出的斜率写出直线BE的方程，把直线BE的方程与椭圆方程联立即可求出直线BE与椭圆的另一交点E的坐标，根据B和E的坐标，利用中点坐标公式求出BE中点的坐标，把中点坐标代入直线l的方程，即可求出n的值．

解答：解：（1）根据椭圆方程得到F₁（-

a2-2

，0），P（

a2-2

，m），
把P的坐标代入椭圆方程得：m²=

4

a2

，
则

F1P

•

OP

=2

a2-2

•

a2-2

+m²=2（a²-2）+

4

a2

=5，解得a²=4，
所以椭圆C方程为：

x2

4

+

y2

2

=1，
（2）由（1）求出的椭圆方程得：B（0，

2

）
BE⊥l，得BE方程的斜率为1，则直线BE的方程为y=x+

2

，
由

y=x+ 2 x2 4 + y2 2 =1

得x=0，或x=-

4 2

3

．
E(-

4 2

3

，-

2

3

)，∴BE中点为(-

2 2

3

，

2

3

)，
把BE的中点坐标代入y=-x+n得：

2

3

=

2 2

3

+n，解得：n=-

2

3

．

点评：此题考查学生掌握椭圆的简单性质，会求椭圆的标准方程，厉害运用平面向量的数量积的运算法则及中点坐标公式化简求值，是一道综合题．