题目内容
已知
,
是单位向量,且
,
的夹角为
,若向量
满足|
-
+2
|=2,则|
|的最大值为( )
| a |
| b |
| a |
| b |
| π |
| 3 |
| c |
| c |
| a |
| b |
| c |
A、2+
| ||
B、2-
| ||
C、
| ||
D、
|
考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:由题意可设
=(1,0),
=(
,
),
=(x,y),可得x2+(y+
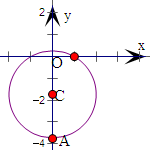
)2=4,故向量
的终点在以C(0,-
)为圆心,半径等于2的圆上,由图象即可得到最大值为|OA|.
| a |
| b |
| 1 |
| 2 |
| ||
| 2 |
| c |
| 3 |
| c |
| 3 |
解答:
 解:
解:
,
是单位向量,且
,
的夹角为
,
设
=(1,0),
=(
,
),
=(x,y)
则
-
+2
=(x,y+
),
∵|
-
+2
|=2,即x2+(y+
)2=4,
故向量
的终点在以C(0,-
)为圆心,半径等于2的圆上,
∴|
|的最大值为|OA|=|OC|+r=
+2.
故选:A.
 解:
解:| a |
| b |
| a |
| b |
| π |
| 3 |
设
| a |
| b |
| 1 |
| 2 |
| ||
| 2 |
| c |
则
| c |
| a |
| b |
| 3 |
∵|
| c |
| a |
| b |
| 3 |
故向量
| c |
| 3 |
∴|
| c |
| 3 |
故选:A.
点评:本题主要考查两个向量的数量积的运算,熟练掌握向量的坐标运算和圆的方程及数形结合是解题的关键,属于基础题.

练习册系列答案
相关题目
已知命题p:存在a∈R,曲线x2+ay2=1为双曲线;命题q:
≤0的解集是{x|1<x<2}.给出下列结论中正确的有( )
①命题“p且q”是真命题; ②命题“p且(?q)”是真命题;
③命题“(?p)或q”为真命题; ④命题“(?p)或(?q)”是真命题.
| x-1 |
| x-2 |
①命题“p且q”是真命题; ②命题“p且(?q)”是真命题;
③命题“(?p)或q”为真命题; ④命题“(?p)或(?q)”是真命题.
| A、1个 | B、2个 | C、3个 | D、4个 |
已知AE是△ABC的中线,若∠A=120°,
•
=-2,则|
|的最小值是( )
| AC |
| AB |
| AE |
| A、-1 | B、0 | C、1 | D、2 |
 如图,在直径为1的圆O中,作一关于圆心对称、邻边互相垂直的十字形,其中y>x>0.
如图,在直径为1的圆O中,作一关于圆心对称、邻边互相垂直的十字形,其中y>x>0. 如图,正△ABC的边长为2,P、Q分别在边AB、AC上运动,且线段PQ将△ABC的面积二等分,求线段PQ长的取值范围.
如图,正△ABC的边长为2,P、Q分别在边AB、AC上运动,且线段PQ将△ABC的面积二等分,求线段PQ长的取值范围.