题目内容
(本题满分13分)已知椭圆
 的焦距为
的焦距为 ,且过点
,且过点 .
.
(1)求椭圆的方程;
(2)已知 ,是否存在
,是否存在 使得点
使得点 关于
关于 的对称点
的对称点 (不同于点
(不同于点 )在椭圆
)在椭圆 上?若存在求出此时直线
上?若存在求出此时直线 的方程,若不存在说明理由.
的方程,若不存在说明理由.
(1) ;(2)不存在k
;(2)不存在k
【解析】
试题分析:(1)由已知,焦距为2c= 1分
1分
又 2分
2分
点 在椭圆C:
在椭圆C:  上,
上, 3分
3分
故,所求椭圆的方程为 5分
5分
(2)当k=0时,直线l:y=-1,点 不在椭圆上; 7分
不在椭圆上; 7分
当k≠0时,可设直线 ,即
,即 8分
8分
代入 整理得
整理得
因为 ,所以
,所以
若A,B关于直线l对称,则其中点 在直线y=kx-1上 10分
在直线y=kx-1上 10分
所以 ,解得k=1因为此时点
,解得k=1因为此时点 在直线l上, 12分
在直线l上, 12分
所以对称点B与点A重合,不合题意,所以不存在k满足条件. 13分
考点:本题考查椭圆的几何性质,椭圆的标准方程,直线与椭圆的位置关系

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
(12分)年龄在60岁(含60岁)以上的人称为老龄人,某小区的老龄人有350人,他们的健康状况如下表:
健康指数 | 2 | 1 | 0 | ﹣1 |
60岁至79岁的人数 | 120 | 133[] | 34 | 13 |
80岁及以上的人数 | 9 | 18 | 14 | 9 |
其中健康指数的含义是:2代表“健康”,1代表“基本健康”,0代表“不健康,但生活能够自理”,﹣1代表“生活不能自理”.
(1)随机访问该小区一位80岁以下的老龄人,该老人生活能够自理的概率是多少?
(2)按健康指数大于0和不大于0进行分层抽样,从该小区的老龄人中抽取5位,并随机地访问其中的3位.求被访问的3位老龄人中恰有1位老龄人的健康指数不大于0的概率.
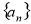 中,前n项和为
中,前n项和为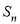 ,已知
,已知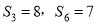 ,则
,则 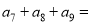 ( )
( )  B.
B. C.
C. D.
D.
 ,
, 满足约束条件
满足约束条件 ,则
,则 的最大值等于 ( )
的最大值等于 ( ) 均为常数
均为常数 ,当
,当 时取极大值,当
时取极大值,当 时取极小值,则
时取极小值,则 的取值范围是
的取值范围是 B.
B. C.
C. D.
D.
 满足
满足 ,且
,且 时,
时, ,则
,则
 C.
C. D.
D.
 分别是正方体
分别是正方体 的棱
的棱 的中点,点
的中点,点 分别在线段
分别在线段 上.以
上.以 为顶点的三棱锥
为顶点的三棱锥 的俯视图不可能是( )
的俯视图不可能是( ) 

 与
与 的夹角是
的夹角是 ,且
,且 ,
, ,若
,若 ,则实数
,则实数 _______.
_______.