题目内容
设f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2,若对任意x∈[a,a+2],不等式f(x+a)≥f(3x+1)恒成立,则实数a的取值范围是 .

【解析】
试题分析:∵当x≥0时,f(x)= ,∴此时函数f(x)单调递增,
,∴此时函数f(x)单调递增,
∵f(x)是定义在R上的奇函数,
∴函数f(x)在R上单调递增,
若对任意x∈[a,a+2],不等式f(x+a)≥f(3x+1)恒成立,
则x+a≥3x+1恒成立,
即a≥2x+1恒成立,
∵x∈[a,a+2],
∴ =2(a+2)+1=2a+5,
=2(a+2)+1=2a+5,
即a≥2a+5,
解得a≤-5,
考点:本题考查函数奇偶性的性质;函数单调性的性质

练习册系列答案
相关题目
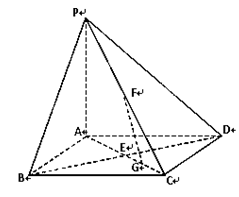
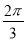 时,求PC与底面ABCD所成角的正切值.
时,求PC与底面ABCD所成角的正切值. ,且
,且 ,则集合
,则集合 可能是( )
可能是( ) B.
B. C.
C. D.
D.

 的焦距为
的焦距为 ,且过点
,且过点 .
. ,是否存在
,是否存在 使得点
使得点 关于
关于 的对称点
的对称点 (不同于点
(不同于点 上?若存在求出此时直线
上?若存在求出此时直线
 的定义域是( )
的定义域是( ) C.[1,4] D.
C.[1,4] D.
 ,则与
,则与 图象相切的斜率最小的切线方程为( )
图象相切的斜率最小的切线方程为( ) (B)
(B)
 (D)
(D)