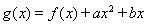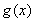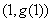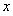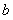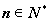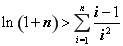ЬтФПФкШн
НќМИФъРД,ЮвЙњаэЖрЕиЧјОГЃГіЯжИЩКЕЯжЯѓ,ЮЊПЙКЕОГЃвЊНјааШЫЙЄНЕгъ.ЯжгЩЬьЦјдЄБЈЕУжЊ,ФГЕидкЮДРД5ЬьЕФжИЖЈЪБМфЕФНЕгъИХТЪЪЧ:ЧА3ЬьОљЮЊ50%,Кѓ2ЬьОљЮЊ80%,5ЬьФкШЮКЮвЛЬьЕФИУжИЖЈЪБМфУЛгаНЕгъ,дђдкЕБЬьЪЕааШЫЙЄНЕгъ,Зёдђ,ЕБЬьВЛЪЕЪЉШЫЙЄНЕгъ.
(1)ЧѓжСЩйга1ЬьашвЊШЫЙЄНЕгъЕФИХТЪ.
(2)ЧѓВЛашвЊШЫЙЄНЕгъЕФЬьЪ§xЕФЗжВМСаКЭЦкЭћ.
(1)  (2) xЕФЗжВМСаЪЧ:
(2) xЕФЗжВМСаЪЧ:
x | 0 | 1 | 2 | 3 | 4 | 5 |
P |
|
|
|
|
|
|
3.1
ЁОНтЮіЁП(1)5ЬьШЋВЛашвЊШЫЙЄНЕгъЕФИХТЪЪЧP1=( )3ЁЄ(
)3ЁЄ( )2=
)2= ,ЙЪжСЩйга1ЬьашвЊШЫЙЄНЕгъЕФИХТЪЪЧ1-P1=1-
,ЙЪжСЩйга1ЬьашвЊШЫЙЄНЕгъЕФИХТЪЪЧ1-P1=1- =
= .
.
(2)xЕФШЁжЕЪЧ0,1,2,3,4,5,гЩ(1)жЊ5ЬьВЛашвЊШЫЙЄНЕгъЕФИХТЪЪЧ:P(x=5)=P1= ,
,
4ЬьВЛашвЊШЫЙЄНЕгъЕФИХТЪЪЧ:
P(x=4)=( )3
)3 ЁС
ЁС +
+ (
( )3(
)3( )2=
)2=
= ,
,
3ЬьВЛашвЊШЫЙЄНЕгъЕФИХТЪЪЧ:
P(x=3)= (
( )3(
)3( )2+
)2+ (
( )3
)3 (
( )(
)( )+(
)+( )3(
)3( )2=
)2= ,
,
2ЬьВЛашвЊШЫЙЄНЕгъЕФИХТЪЪЧ:
P(x=2)= (
( )3(
)3( )2+
)2+ (
( )3
)3 (
( )ЁС(
)ЁС( )+(
)+( )3ЁС(
)3ЁС( )2=
)2= ,
,
1ЬьВЛашвЊШЫЙЄНЕгъЕФИХТЪЪЧ:
P(x=1)= (
( )3(
)3( )2+(
)2+( )3
)3 (
( )(
)( )=
)= ,
,
0ЬьВЛашвЊШЫЙЄНЕгъЕФИХТЪЪЧ:
P(x=0)=( )3(
)3( )2=
)2= ,
,
ЙЪВЛашвЊШЫЙЄНЕгъЕФЬьЪ§xЕФЗжВМСаЪЧ:
x | 0 | 1 | 2 | 3 | 4 | 5 |
P |
|
|
|
|
|
|
ВЛашвЊШЫЙЄНЕгъЕФЬьЪ§xЕФЦкЭћЪЧ:
E(x)=0ЁС +1ЁС
+1ЁС +2ЁС
+2ЁС +3ЁС
+3ЁС +4ЁС
+4ЁС +5ЁС
+5ЁС =3.1.
=3.1.
ЁОЗНЗЈММЧЩЁПЧѓРыЩЂаЭЫцЛњБфСПОљжЕгыЗНВюЕФЛљБОЗНЗЈ
(1)ЖЈвхЗЈ:вбжЊЫцЛњБфСПЕФЗжВМСаЧѓЫќЕФОљжЕЁЂЗНВюКЭБъзМВю,ПЩжБНгАДЖЈвх(ЙЋЪН)ЧѓНт.
(2)аджЪЗЈ:вбжЊЫцЛњБфСПІЮЕФОљжЕгыЗНВю,ЧѓІЮЕФЯпадКЏЪ§ІЧ=aІЮ+bЕФОљжЕгыЗНВю,ПЩжБНгРћгУОљжЕЁЂЗНВюЕФаджЪЧѓНт.
(3)ЙЋЪНЗЈ:ШчФмЗжЮіЫљИјЫцЛњБфСПЪЧЗўДгГЃгУЕФЗжВМ(ШчСНЕуЗжВМ,ЖўЯюЗжВМЕШ),ПЩжБНгРћгУЫќУЧЕФОљжЕЁЂЗНВюЙЋЪНЧѓНт.

ЙигкЯпадЛиЙщ,вдЯТЫЕЗЈДэЮѓЕФЪЧ(ЁЁЁЁ)
(A)здБфСПШЁжЕвЛЖЈЪБ,вђБфСПЕФШЁжЕДјгавЛЖЈЫцЛњадЕФСНИіБфСПжЎМфЕФЙиЯЕНазіЯрЙиЙиЯЕ
(B)дкЦНУцжБНЧзјБъЯЕжагУУшЕуЕФЗНЗЈЕУЕНЕФБэЪООпгаЯрЙиЙиЯЕЕФСНИіБфСПЕФвЛзщЪ§ОнЕФЭМаЮНазіЩЂЕуЭМ
(C)ЯпадЛиЙщжБЯпЗНГЬзюФмДњБэЙлВтжЕx,yжЎМфЕФЙиЯЕ,ЧвЦфЛиЙщжБЯпвЛЖЈЙ§бљБОжааФЕу(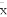 ,
,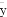 )
)
(D)МзЁЂввЁЂБћЁЂЖЁЫФЮЛЭЌбЇИїздЖдA,BСНБфСПЕФЯпадЯрЙиадзїЪдбщ,ВЂгЩЛиЙщЗжЮіЗЈЗжБ№ЧѓЕУЯрЙиЯЕЪ§rxyШчЯТБэ
| Мз | вв | Бћ | ЖЁ |
rxy | 0.82 | 0.78 | 0.69 | 0.85 |
дђМзЭЌбЇЕФЪдбщНсЙћЬхЯжA,BСНБфСПИќЧПЕФЯпадЯрЙиад