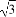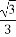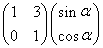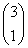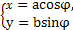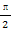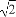Question

已知矩阵A=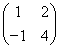,向量α=.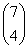

(1)求A的特征值λ1,λ2和对应的特征向量α1,α2.

(2)计算A5α的值.

 

Answer 1

(1) 当λ1=2时,解得α1=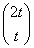(t≠0),当λ2=3时,解得α2=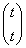(t≠0)

(2) A5α= 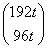+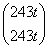=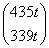(t≠0)

【解析】(1)矩阵A的特征多项式为

λ2-5λ+6,由λ2-5λ+6=0,解得λ1=2,λ2=3.

当λ1=2时,解得α1=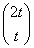(t≠0),当λ2=3时,解得α2=(t≠0).

(2)由α=mα1+nα2得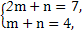解得m=3,n=1.

则A5α=A5(3α1+α2)

=3(A5α1)+A5α2

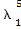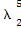=3(α1)+α2

=3×25α1+35α2

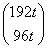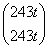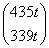=+=(t≠0).