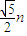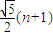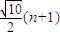Question

对于满足条件a₁²+a_n+1²≤1的所有等差数列|a_n|中，a₁+a₂+…+a_n+1的最大值为（　　）

• A、

  2

  2

  （n+1）
• B、

  2

  2

  n
• C、

  1

  2

  （n+1）
• D、

  1

  2

  n

Answer 1

分析：欲求a₁+a₂+…+a_n+1的最大值，必使得各项最大，由a₁²+a_n+1²≤1恒成立，可以利用基本不等式求得各项的最大值

解答：解：由题意可得：a₁²+a_n+1²≤1，
所以故有2a₁a_n+1≤a₁²+a_n+1²≤1当且仅当a₁=a_n+1时，取到等号，
故使得a₁+a₂+…+a_n的最大值时，数列各项都是

2

2

，
故a₁+a₂+…+a_n+1的最大值为

2

2

（n+1）
故选A．

点评：本题考点是等差数列的性质，考查等差数列的性质与基本不等式的综合使用．