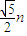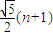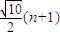题目内容
对于满足条件a12+an+12≤1的所有等差数列{an}中,an+1+an+2+…a2n+1的最大值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:欲求an+1+an+2+…a2n+1的最大值,先由等差数列的求和公式得到an+1+an+2+…+a2n+1=(n+1)
,再由柯西不等式即可得到答案
| 3an+1-a1 |
| 2 |
解答:解:an+1+an+2+…+a2n+1=(n+1)
=(n+1)
=(n+1)
由柯西不等式得3an+1-a1≤
(an+1 2+a1 2)=
所以an+1+an+2+…+a2n+1≤
(n+1)
故选D.
| an+1+a2n+1 |
| 2 |
| an+1+2an+1-a1 |
| 2 |
| 3an+1-a1 |
| 2 |
由柯西不等式得3an+1-a1≤
| 32+(-1)2 |
| 10 |
所以an+1+an+2+…+a2n+1≤
| ||
| 2 |
故选D.
点评:本题考点是柯西不等式及等差数列的性质,灵活转化选用解答方法是解题的关键.

练习册系列答案
相关题目
对于满足条件a12+an+12≤1的所有等差数列|an|中,a1+a2+…+an+1的最大值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|