题目内容
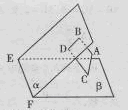
一个棱长为 的正方体的八个顶角上分别截去一个三棱锥,使截掉棱锥后的多面体有六个面为正八边形,八个面为正三角形(如图所示),
的正方体的八个顶角上分别截去一个三棱锥,使截掉棱锥后的多面体有六个面为正八边形,八个面为正三角形(如图所示),
(1)求异面直线 与
与 所成角的大小;
所成角的大小;
(2)求此多面体的体积(结果用最简根式表示).
 的正方体的八个顶角上分别截去一个三棱锥,使截掉棱锥后的多面体有六个面为正八边形,八个面为正三角形(如图所示),
的正方体的八个顶角上分别截去一个三棱锥,使截掉棱锥后的多面体有六个面为正八边形,八个面为正三角形(如图所示),(1)求异面直线
 与
与 所成角的大小;
所成角的大小;(2)求此多面体的体积(结果用最简根式表示).

解: (1) 易知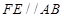 ,
,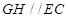 ,
,
所以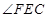 就是异面直线
就是异面直线 与
与 所成的余角). 3分
所成的余角). 3分
经计算得: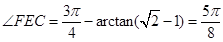
(也可以直接用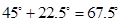 做)
做)
所以异面直线 与
与 所成的角的大小为
所成的角的大小为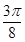
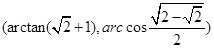 . 6分
. 6分
(2)设正八边形的边长为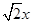 ,则由题意得:
,则由题意得: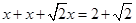 ,
,
所以,正八边形的边长为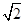 . 9分
. 9分
设多面体的体积为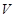 ,
,
则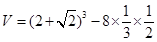 =
=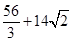 . 12分
. 12分
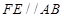 ,
,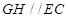 ,
,所以
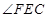 就是异面直线
就是异面直线 与
与 所成的余角). 3分
所成的余角). 3分经计算得:
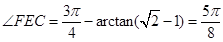
(也可以直接用
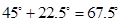 做)
做)所以异面直线
 与
与 所成的角的大小为
所成的角的大小为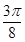
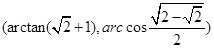 . 6分
. 6分(2)设正八边形的边长为
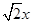 ,则由题意得:
,则由题意得: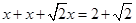 ,
,所以,正八边形的边长为
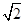 . 9分
. 9分设多面体的体积为
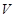 ,
,则
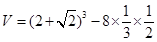 =
=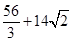 . 12分
. 12分略

练习册系列答案
相关题目
 为不重合的平面,
为不重合的平面, 为不重合的直线,则下列命题正确的是( )
为不重合的直线,则下列命题正确的是( ) ,
, ,
, ,则
,则
 ,
, ,
, ,则
,则
 ,
, ,
, ,
, ,
, ,则
,则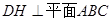 垂足为
垂足为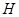 ,
,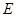 是
是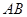 的中点且
的中点且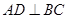 ,
,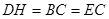 ,
,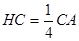 .
.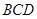
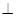 平面
平面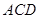 ;
;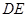 与平面
与平面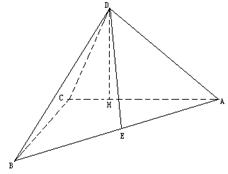
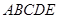 中,
中,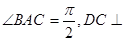 平面
平面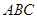 ,
,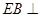 平面
平面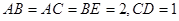 .
.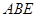 与平面
与平面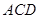 的交线为直线
的交线为直线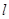 ,求证:
,求证: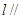 平面
平面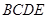 ;
;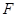 是
是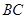 的中点,求证:平面
的中点,求证:平面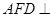 平面
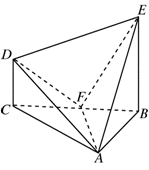
平面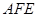 ;
;
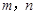 是两条不同直线,
是两条不同直线,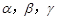 是三个不同平面,正确命题的个数是( )
是三个不同平面,正确命题的个数是( )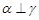 ,
,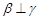 ,则
,则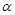 //
//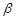 ②若
②若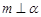 ,
,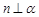 ,则
,则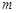 //
//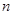
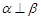 ,
,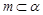 ,则
,则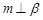 ④若
④若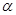 ,
,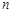 //
//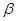 ,则
,则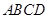 中,对角线
中,对角线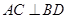 ,且
,且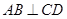 ,则点
,则点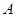 在
在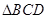 内的射影
内的射影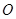 是
是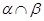 =EF,AB
=EF,AB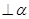 ,CD
,CD