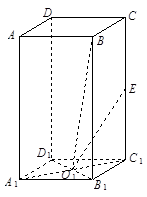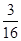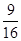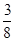题目内容
在几何体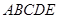 中,
中,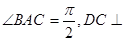 平面
平面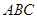 ,
,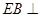 平面
平面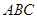 ,
,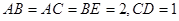 .
.
(1)设平面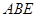 与平面
与平面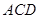 的交线为直线
的交线为直线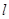 ,求证:
,求证: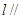 平面
平面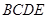 ;
;
(2)设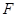 是
是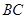 的中点,求证:平面
的中点,求证:平面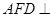 平面
平面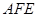 ;
;
(3)求几何体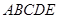 的体积.
的体积.
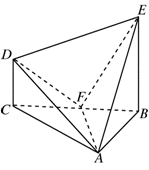
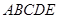 中,
中,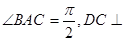 平面
平面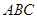 ,
,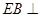 平面
平面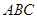 ,
,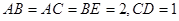 .
.(1)设平面
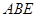 与平面
与平面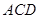 的交线为直线
的交线为直线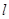 ,求证:
,求证: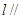 平面
平面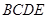 ;
;(2)设
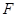 是
是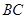 的中点,求证:平面
的中点,求证:平面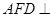 平面
平面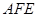 ;
;(3)求几何体
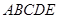 的体积.
的体积.
(1)∵CD⊥平面ABC,BE⊥平面ABC,
∴CD∥BE. ∵CD?平面ABE,
BE?平面ABE, ∴CD∥平面ABE.
又l=平面ACD∩平面ABE,∴CD∥l.
又l?平面BCDE,CD?平面BCDE,
∴l∥平面BCDE.
(2)在△DFE中,FD=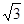 ,FE=
,FE=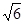 ,DE=3. ∴FD⊥FE.
,DE=3. ∴FD⊥FE.
∵CD⊥平面ABC,∴CD⊥AF, 又BC⊥AF,CD∩BC=C,∴AF⊥平面BCDE,
∴AF⊥FD,∵EF∩AF=F, ∴FD⊥平面AFE.
又FD?平面AFD,∴平面AFD⊥平面AFE.
(3)∵DC⊥平面ABC,BE⊥平面ABC,∴DC∥BE
∵AB=AC=2,且∠BAC=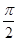 ∴BC=2
∴BC=2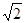
∴S?BEDC=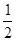 (DC+BE)×BC=3
(DC+BE)×BC=3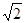
由(2)知AF⊥平面BCED ∴VE-BCDE=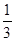 SBED
SBED C AF=
C AF=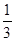 ×3
×3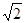 ×
×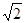 =2.
=2.
∴CD∥BE. ∵CD?平面ABE,
BE?平面ABE, ∴CD∥平面ABE.
又l=平面ACD∩平面ABE,∴CD∥l.
又l?平面BCDE,CD?平面BCDE,
∴l∥平面BCDE.
(2)在△DFE中,FD=
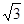 ,FE=
,FE=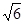 ,DE=3. ∴FD⊥FE.
,DE=3. ∴FD⊥FE.∵CD⊥平面ABC,∴CD⊥AF, 又BC⊥AF,CD∩BC=C,∴AF⊥平面BCDE,
∴AF⊥FD,∵EF∩AF=F, ∴FD⊥平面AFE.
又FD?平面AFD,∴平面AFD⊥平面AFE.
(3)∵DC⊥平面ABC,BE⊥平面ABC,∴DC∥BE
∵AB=AC=2,且∠BAC=
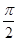 ∴BC=2
∴BC=2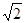
∴S?BEDC=
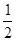 (DC+BE)×BC=3
(DC+BE)×BC=3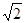
由(2)知AF⊥平面BCED ∴VE-BCDE=
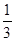 SBED
SBED C AF=
C AF=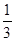 ×3
×3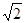 ×
×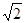 =2.
=2.略

练习册系列答案
相关题目
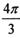 ,则A、B两点的球面距离为________
,则A、B两点的球面距离为________ 的正方体的八个顶角上分别截去一个三棱锥,使截掉棱锥后的多面体有六个面为正八边形,八个面为正三角形(如图所示),
的正方体的八个顶角上分别截去一个三棱锥,使截掉棱锥后的多面体有六个面为正八边形,八个面为正三角形(如图所示), 与
与 所成角的大小;
所成角的大小;

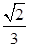
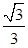
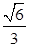
 是
是 的三条高的交点,
的三条高的交点, 平面
平面 ,则下列结论中正确的个数是( )
,则下列结论中正确的个数是( ) ②
② ③
③

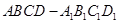 中,
中,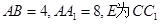 的中点,
的中点,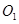 为下底面正方形的中心,
为下底面正方形的中心,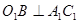 ;
;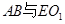 所成角的余弦值;
所成角的余弦值;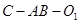 的余弦值.
的余弦值.