题目内容
1.在△ABC中,角A,B,C的对边分别为a,b,c,已知$A={60°},b=4,{S_{△ABC}}=4\sqrt{3}$,则a=4.分析 由已知利用三角形面积公式可求c的值,进而利用余弦定理即可解得a的值.
解答 解:∵$A={60°},b=4,{S_{△ABC}}=4\sqrt{3}$=$\frac{1}{2}$bcsinA=$\frac{1}{2}×4×c×$$\frac{\sqrt{3}}{2}$,
∴解得c=4,
∴a=$\sqrt{{b}^{2}+{c}^{2}-2bccosA}$=$\sqrt{{4}^{2}+{4}^{2}-2×4×4×\frac{1}{2}}$=4.
故答案为:4.
点评 本题主要考查了三角形面积公式,余弦定理在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
相关题目
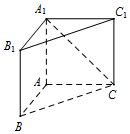 如图,直三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC.若AB=AC=AA1=1,BC=$\sqrt{2}$,则异面直线A1C与B1C1所成的角为$\frac{π}{3}$..
如图,直三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC.若AB=AC=AA1=1,BC=$\sqrt{2}$,则异面直线A1C与B1C1所成的角为$\frac{π}{3}$..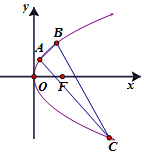 给定直线l:y=2x-16,抛物线G:y2=ax(a>0)
给定直线l:y=2x-16,抛物线G:y2=ax(a>0)