题目内容
14.已知函数y=$\frac{3x}{x+2}$(1)若0≤y≤1,求自变量x的取值范围
(2)若0≤x≤4,求函数值y的取值范围.
分析 (1)利用分式函数的性质解不等式0≤y≤1,即可求自变量x的取值范围
(2)若0≤x≤4,根据分式函数的单调性即可得到结论.
解答 解:(1)y=$\frac{3x}{x+2}$=$\frac{3(x+2)-6}{x+2}$=3-$\frac{6}{x+2}$,
若0≤y≤1,
则0≤3-$\frac{6}{x+2}$≤1,
即-3≤-$\frac{6}{x+2}$≤-2,
即2≤$\frac{6}{x+2}$≤3,
$\frac{1}{3}≤$$\frac{x+2}{6}$$≤\frac{1}{2}$,
即2≤x+2≤3,
解得0≤x≤1,即自变量x的取值范围是[0,1].
(2)∵y=$\frac{3x}{x+2}$=$\frac{3(x+2)-6}{x+2}$=3-$\frac{6}{x+2}$,在[0,4]上为增函数
∴当x=0时,y最小,y=0,
当x=4时,y最大,y=$\frac{3×4}{4+2}=\frac{12}{6}$=2,
即0≤y≤2,
即函数值y的取值范围是[0,2].
点评 本题主要考查分式函数的性质,利用分子常数化,结合函数的单调性是解决本题的关键.

练习册系列答案
相关题目
5.已知全集U={0,1,2,3,4},A={1,2,3},B={0,2}则A∩(∁UB)等于( )
| A. | { 1,2,3,4} | B. | { 0,1,2,3 } | C. | { 1,2 } | D. | { 1,3 } |
2.已知函数f(x)=x2+3x-21nx,则函数f(x)的单调递减区间为( )
| A. | (-2,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,+∞] | C. | (-∞,-2) | D. | (0,$\frac{1}{2}$) |
5.函数y=$\frac{1}{{x}^{2}+2}$的值域为( )
| A. | R | B. | [$\frac{1}{2}$,+∞) | C. | (-∞,$\frac{1}{2}$] | D. | (0,$\frac{1}{2}$] |
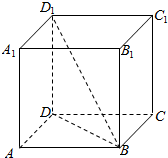 在正方体ABCD-A1B1C1D1中,对角线BD1分别与平面AC,平面BC1,平面BA1所成的角,并求这些角的余弦值.
在正方体ABCD-A1B1C1D1中,对角线BD1分别与平面AC,平面BC1,平面BA1所成的角,并求这些角的余弦值. 已知直线AC与圆O相切于点B,AD交圆O于F,D两点,CF交圆O于E,F两点,BD∥CE,AB=BC,AD=2,BD=1,则CE=4.
已知直线AC与圆O相切于点B,AD交圆O于F,D两点,CF交圆O于E,F两点,BD∥CE,AB=BC,AD=2,BD=1,则CE=4.