题目内容
9.设不等式-x2+(1-b)x+b>0的解集为{x|1<x<2},求不等式bx≥4的解集.分析 根据一元二次不等式的解集和一元二次方程之间的关系求出b,即可得到结论.
解答 解:∵不等式-x2+(1-b)x+b>0的解集为{x|1<x<2},
∴1,2是对应方程-x2+(1-b)x+b=0的两个根,
则1×2=-b,
即b=-2,
则不等式bx≥4等价为-2x≥4,
即x≤-2,
即不等式的解集为(-∞,-2].
点评 本题主要考查一元二次不等式和一元一次不等式的解法,根据一元二次不等式与一元二次方程之间的关系求出b是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知$\frac{1-tanα}{1+tanα}$=2,则tan(α+$\frac{π}{4}$)=( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
20.在极坐标系中,曲线C的方程为F(ρ,θ)=0,则F(ρ0,θ0)=0是点P(ρ0,θ0)在曲线C上的( )
| A. | 充要条件 | B. | 充分非必要条件 | ||
| C. | 必要非充分条件 | D. | 非充分非必要条件 |
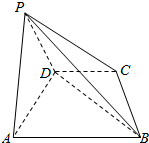 四棱锥P-ABCD中,△PAD为等边三角形,底面ABCD为等腰梯形,满足AB∥CD,AD=DC=$\frac{1}{2}$AB=2,且平面PAD⊥平面ABCD.
四棱锥P-ABCD中,△PAD为等边三角形,底面ABCD为等腰梯形,满足AB∥CD,AD=DC=$\frac{1}{2}$AB=2,且平面PAD⊥平面ABCD.