题目内容
7.数列{an}满足an+1=(2|sin$\frac{nπ}{2}$|-1)an+2n,则数列{an}的前100项和为( )| A. | 5050 | B. | 5100 | C. | 9800 | D. | 9850 |
分析 由已知数列递推式求出S4,S8-S4,S12-S8的值,可得数列{an}的前100项满足S4,S8-S4,S12-S8,…是以12为首项,16为公差的等差数列,再由等差数列的前n项和求解.
解答 解:由an+1=(2|sin$\frac{nπ}{2}$|-1)an+2n,得:
a1=a1,
a2=a1+2,
a3=-a2+4=-a1+2,
a4=a3+6=-a1+8,
∴a1+a2+a3+a4=12;
同理求得a5+a6+a7+a8=28;
a9+a10+a11+a12=44;
∵$\frac{100}{4}=25$,
∴数列{an}的前100项满足S4,S8-S4,S12-S8,…是以12为首项,16为公差的等差数列,
则数列{an}的前100项和为S=25×12+$\frac{25×24×16}{2}$=5100.
故选:B.
点评 本题考查数列递推式,考查等差关系的确定,训练了等差数列前n项和的求法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.函数y=f(x)满足对任意x∈R都有f(x+2)=f(-x)成立,且函数y=f(x-1)的图象关于点(1,0)对称,f(1)=4,则f(2016)+f(2017)+f(2018)=( )
| A. | 12 | B. | 8 | C. | 4 | D. | 0 |
12.已知函数f(x)=aex-2x-2a,且a∈[1,2],设函数f(x)在区间[0,ln2]上的最小值为m,则m的取值范围是( )
| A. | [-2,-2ln2] | B. | [-2,-$\frac{1}{e}$] | C. | [-2ln2,-1] | D. | [-1,-$\frac{1}{e}$] |
19.已知实数x、y满足不等式组$\left\{\begin{array}{l}y≥1\\ x-y≥0\\ x+2y-6≤0\end{array}\right.$时,目标函数z=2x+y的最大值为( )
| A. | 3 | B. | 6 | C. | 8 | D. | 9 |
16.在复平面内,复数z=$\frac{3+5i}{1+i}$(i为虚数单位)对应点的坐标是( )
| A. | (1,4) | B. | (4,-1) | C. | (4,1) | D. | (-1,4) |
17.下列关于命题的说法错误的是( )
| A. | 命题“若x2-3x+2=0,则x=2”的逆否命题为“若x≠2,则x2-3x+2≠0” | |
| B. | “a=2”是“函数f(x)=logax在区间(0,+∞)上为增函数”的充分不必要条件 | |
| C. | 若命题p:?n∈N,2n>1000,则¬p:?n∈N,2n>1000 | |
| D. | 命题“?x∈(-∞,0),2x<3x”是假命题 |
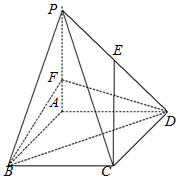 如图,在四棱锥 P-ABCD 中,底面 ABCD是菱形,PA⊥平面 ABCD,PA=3,F 是棱 PA 上的一个动点,E 为 PD 的中点.
如图,在四棱锥 P-ABCD 中,底面 ABCD是菱形,PA⊥平面 ABCD,PA=3,F 是棱 PA 上的一个动点,E 为 PD 的中点.