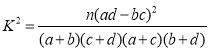题目内容
【题目】已知点![]() ,直线
,直线![]() :
:![]() ,
,![]() 为平面上的动点,过点
为平面上的动点,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,且满足
,且满足![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与轨迹
与轨迹![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为直线
为直线![]() 上一点,且满足
上一点,且满足![]() ,若
,若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】分析:(1)设![]() ,则
,则![]() ,利用
,利用![]() ,即可求解轨迹
,即可求解轨迹![]() 的方程;
的方程;
(II)设![]() 的方程为
的方程为![]() ,联立方程组,求得
,联立方程组,求得![]() ,又由
,又由![]() ,得到点
,得到点![]() ,在利用弦长公式和点到直线的距离公式,即可表达
,在利用弦长公式和点到直线的距离公式,即可表达![]() 的面积,求得
的面积,求得![]() 的值,进而得到直线的方程;
的值,进而得到直线的方程;
详解:(1)设![]() ,则
,则![]() ,
,![]()
![]() ,
,![]() ,
,
![]() ,
,![]() ,即轨迹
,即轨迹![]() 的方程为
的方程为![]() .
.
(2)法一:显然直线![]() 的斜率存在,设
的斜率存在,设![]() 的方程为
的方程为![]() ,
,
由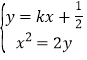 ,消去
,消去![]() 可得:
可得:![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
即![]()
![]() ,
,
![]() ,即
,即![]()
![]()
![]() ,
,![]() ,即
,即![]() ,
,
![]()
![]() ,
,
![]()
![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
![]() ,解得
,解得![]() ,
,
![]() 直线
直线![]() 的方程为
的方程为![]() 或
或![]() .
.
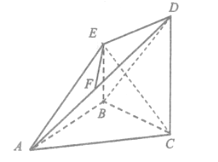
法2:(Ⅱ)设![]() ,AB的中点为
,AB的中点为![]()
则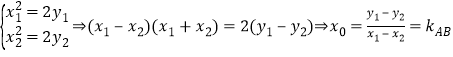
直线![]() 的方程为
的方程为![]() ,
,
过点A,B分别作![]() ,因为
,因为![]() 为AB 的中点,
为AB 的中点,
所以在![]() 中,
中,![]()
故![]() 是直角梯形
是直角梯形![]() 的中位线,可得
的中位线,可得![]() ,从而
,从而![]()
点![]() 到直线
到直线![]() 的距离为:
的距离为:![]()
因为E点在直线![]() 上,所以有
上,所以有![]() ,从而
,从而![]()
由![]() 解得
解得![]()
所以直线![]() 的方程为
的方程为![]() 或
或![]() .
.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
【题目】为了调查某生产线上质量监督员甲是否在现场对产品质量好坏有无影响,现统计数据如下:质量监督员甲在现场时,1 000件产品中合格品有990件,次品有10件,甲不在现场时,500件产品中有合格品490件,次品有10件.
(1)补充下面列联表,并初步判断甲在不在现场与产品质量是否有关:
合格品数/件 | 次品数/件 | 总数/件 | |
甲在现场 | 990 | ||
甲不在现场 | 10 | ||
总数/件 |
(2)用独立性检验的方法判断能否在犯错误的概率不超过0.15的前提下认为“甲在不在现场与产品质量有关”?
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |